Distorsion d'amplitude d'interférence
J'ai parlé de l'analyse COM et de canal dans des blogs précédents, et j'aimerais continuer la discussion avec plus d'aides visuelles et quelques exemples de code pour permettre aux lecteurs de faire eux-mêmes certaines analyses.
Pour commencer, revoyons ce qu'est le COM et une vue d'ensemble de haut niveau de comment le COM est calculé. Le COM est un rapport signal-sur-bruit de tension à un moment donné. Le moment est le point d'échantillonnage, et le signal disponible est la tension de la réponse à l'impulsion au point d'échantillonnage. Une réponse à l'impulsion est la forme de la tension après avoir traversé le canal à l'essai, et l'impulsion est simplement une fonction rect avec un intervalle unitaire qui correspond au débit de données souhaité.
Le bruit est trouvé par analyse statistique et est divisé en trois catégories principales : ISI, Diaphonie, et Système.

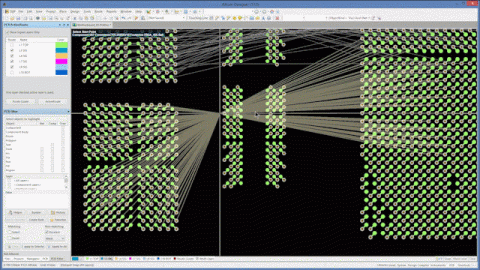
Le bruit ISI est le bruit statistique provenant des réflexions dans le canal. Chaque valeur non nulle dans la réponse impulsionnelle après les robinets DFE ajoute à ce bruit. Les seules valeurs prises en compte sont espacées de M points les unes des autres. Ceci est visible dans la figure ci-dessous sous forme de cercles. Les cercles magenta représentent les contributions de bruit qui ont été prises en charge par le DFE, et les cercles noirs sont les valeurs de bruit qui n'ont pas été traitées par le DFE.

Le diaphonie est traitée de la même manière sauf que la valeur de bruit est asynchrone. Cela signifie que COM prend la valeur de diaphonie maximale au lieu de la valeur qui correspond à la tranche de signal disponible. Le bruit du système contient le jitter dépendant des données (DDJ), le jitter aléatoire, et une valeur globale de bruit provenant du CI. Le DDJ est lié aux réflexions donc il suit la tendance de la valeur de bruit ISI : plus d'ISI signifie plus de DDJ. Cependant, tout autre bruit du système est constant, indépendamment du canal.
Effectuer les calculs pour créer la réponse impulsionnelle n'est en aucun cas facile, mais la plupart des ingénieurs et scientifiques peuvent finalement y arriver. Cependant, la partie bruit du problème est beaucoup plus difficile. Le principal problème est la mise en œuvre de l'équation 93A-39 que j'ai ci-dessous.
Pour la plupart des gens, ceci est une équation assez intimidante. Je vais expliquer chaque partie puis montrer quelques aides visuelles. En commençant de gauche à droite, pn(y) est la probabilité que la tension se trouve à l'emplacement y de l'échantillon contributif, n. En d'autres termes, c'est la probabilité qu'une certaine quantité de bruit se produise pour l'un des points de la réponse impulsionnelle. 1/L prend en compte la modulation. Chaque niveau a sa propre probabilité, et la probabilité totale dans la direction y doit s'ajouter à un. Ainsi, la probabilité est répartie également pour chaque niveau. Dans cet article, je vais analyser le Non-Return Zero (NRZ), la Modulation d'Amplitude d'Impulsion 4 (PAM4) et PAM6. Pour le NRZ, il y a deux niveaux, PAM4 a quatre niveaux, et PAM6 a 6 niveaux. En pratique, le code IEEE COM n'évalue la fonction de distribution de probabilité (PDF) que pour un niveau, car la norme ne prend pas en compte les niveaux asymétriques (mais cela pourrait 😉). Ne considérer qu'un seul niveau améliore également la vitesse d'exécution, ce qui a été un sujet brûlant dans la norme.
Passons un moment sur la fonction delta et intéressons-nous à son argument :. La seule chose importante ici est que l'argument est nul lorsque y est identique à
. Enfin, il y a la fonction delta : , et la fonction delta est simplement un lorsque son argument est nul.
Donc, si nous balayons sur y, vous obtenez la PDF de combien de bruit l'échantillon n va créer. L'étape suivante consiste à utiliser l'équation 93A-40 pour chaque échantillon n et vous obtenez la PDF du bruit provenant de la source en temps réel.
Je vais appliquer cette équation à l'échantillon montré ci-dessous. C'est un point où le signal ré-réfléchi crée du bruit sur le canal de 0,000819779 volts.

En traçant l'argument intérieur de 93A-39, vous obtenez le graphique suivant. Vous pouvez voir qu'il y a un croisement à zéro à la fois pour l = 0 et l = 1, et que le croisement est à +/-0,000819779. Ces points de croisement à zéro sont où pn(y) = 1/L.

Si nous traçons ensuite cette PDF, nous obtenons le graphique suivant.

La même analyse peut être réalisée pour d'autres schémas de modulation, et j'ai ci-dessous NRZ, PAM4, PAM6 et PAM8. La probabilité de chaque source de bruit diminue à mesure que la modulation augmente, et il y a plus de sources de bruit à mesure que la modulation augmente.

Vous appliquez ensuite l'équation 93A-40 pour chaque échantillon pertinent et vous obtenez une distribution appropriée. L'animation ci-dessous montre la distribution en cours de réalisation. La ligne noire indique le point d'échantillon n considéré et la PDF se met à jour à mesure que la ligne se déplace. J'ai normalisé la PDF pour que le pic soit à un afin que l'animation soit claire, mais la somme de la PDF doit être égale à un pour qu'elle soit valide. Remarquez comment la PDF se disperse à mesure que le point d'échantillon se déplace le long du bruit entre 5 et 6 ns. C'est exactement ainsi que les réflexions causent du bruit dans le système. Le niveau du bruit est assez faible et remarquez comment il augmente de manière spectaculaire la largeur du bruit.

La question évidente suivante est : « comment la modulation affecte-t-elle la quantité de bruit ? » Ajouter des niveaux augmentera-t-il le bruit, ou diminuer la probabilité de chaque niveau réduira-t-il le bruit total ? Il s'avère qu'il y a moins de bruit d'ISI à mesure que la modulation augmente. Le graphique ci-dessous montre la PDF de cette réponse impulsionnelle égalisée pour NRZ, PAM4, PAM6 et PAM8.

Cela semble indiquer que monter en modulation réduit le bruit. Alors, pourquoi ne pas simplement augmenter la modulation pour obtenir des débits de données plus élevés ! Eh bien, ce n'est pas si simple, et je vais en parler plus en détail ci-dessous.
J'ai mentionné plus tôt que la somme des PDF doit être égale à un pour qu'elle soit valide, et si vous implémentez ce code dans MATLAB, vous remarquerez quelque chose d'étrange à mesure que L augmente.
| L | Somme de p |
|---|---|
| 2 | 1 |
| 4 | 1 |
| 6 | 0.026084 |
| 8 | 1.2496e-5 |
Que s'est-il passé ? Il s'avère que les nombres sont si petits que la double précision n'est pas suffisante pour capturer le PDF, et lorsqu'il est créé, vous perdez certaines informations. Heureusement, il existe une solution à ce problème. Sachant que la somme doit être égale à un, vous pouvez simplement diviser le PDF par la somme de p et vous forcerez ce comportement, et c'est exactement ce que fait le code COM publié par l'IEEE. Sinon, vous auriez besoin d'implémenter une échelle de précision supérieure dans MATLAB. Cela ralentirait le code sans réel avantage.
Le code pour créer cette distribution et un script d'exemple pour l'exécuter ont été publiés ici.
Nous avons vu que nous pouvons utiliser cette équation d'interférence pour comprendre comment les réflexions provoquent une dégradation du signal. Prenons les choses un peu plus loin et explorons l'égalisation par retour de décision (DFE). La spécification IEEE indique combien d'échantillons seront corrigés par le DFE. La variable pour les échantillons est Nb, et j'ai fixé Nb à 12 pour tous les exemples dans cet article. Tant que la tension de bruit est en dessous d'un seuil, le code COM considère ces échantillons comme nuls et annule le bruit, mais qu'arrive-t-il aux autres échantillons ?

Les DFE qui affectent des échantillons autres que la tranche de signal disponible sont généralement soit des fonctions rect idéales, soit des réponses d'impulsion mises à l'échelle. Que se passe-t-il si vous prenez les amplitudes d'impulsion définies par les lignes vertes, et les utilisez pour éliminer le bruit ? Vous obtenez le graphique ci-dessous. Le premier échantillon de bruit a été éliminé, mais l'impulsion utilisée pour corriger le bruit cause également du bruit supplémentaire !

Les robinets DFE doivent être créés séquentiellement au lieu de tous en même temps. Si nous faisons cela, nous obtenons effectivement aucun bruit au point d'échantillonnage, et les autres points ont un bruit résiduel qui affecte le signal à d'autres tranches. L'animation ci-dessous montre ce processus.

Maintenant que nous avons une réponse impulsionnelle égalisée avec et sans DFE, nous pouvons balayer le point d'échantillonnage pour créer des motifs d'œil statistiques et voir comment exactement le DFE affecte la qualité du signal. Ci-dessous, j'ai des motifs d'œil pour NRZ, PAM4 et PAM6 pour des réponses impulsionnelles égalisées et des réponses impulsionnelles égalisées avec le DFE. Et tout comme avant, vous pouvez balayer les points d'échantillonnage et observer la création du motif d'œil. Cela permet des observations intéressantes, mais dans ce cas, je n'ai qu'une trace. Je pense que ce serait plus excitant si j'appliquais cela à un fond de panier. Cependant, je n'ai pas de fond de panier bruyant à analyser, donc cela devra suffire pour aujourd'hui.
La création de l'œil PAM6

NRZ - Avant et après DFE (25G)


PAM4 - Avant et après DFE (50G)


PAM6 - Avant et après DFE (75G)


Faisons quelques observations à partir de ces graphiques. Premièrement, remarquez à quel point le motif d'œil s'améliore grâce au DFE. Le motif d'œil NRZ égalisé fonctionnerait probablement très bien sans un DFE, mais les yeux PAM4 et PAM6 sont complètement fermés avant que le DFE soit mis en œuvre.
La deuxième observation concerne la manière dont la largeur de l'œil diminue de façon spectaculaire avec la modulation. À vue d'œil (jeu de mots voulu), la largeur de l'œil diminue de 50 % avec chaque modulation ajoutée. Cela signifie que non seulement il sera plus difficile pour le système de détecter la valeur appropriée dans la direction de la tension, mais le point d'échantillonnage doit être de plus en plus stable avec une modulation accrue.
Enfin, observez la hauteur de l'œil dans l'œil PAM6. Cela suppose que l'émetteur peut parfaitement créer des niveaux également distribués et qu'il n'y a pas de bruit de système. Ajouter du bruit de système et des niveaux asymétriques rendra cela très difficile à résoudre avec un faible TEB, et cela explique pourquoi nous avons besoin de la correction d'erreur en avant (FEC) à des débits de données et des schémas de modulation plus élevés. Vous ne pouvez tout simplement pas obtenir une transmission sans erreur sans cela.
Cela conclut notre bilan pour ce trimestre. Alors, qu'avons-nous appris ? Le code source ouvert est disponible sur le site de MATHWORKS pour créer des PDF de distorsion d'aptitude à l'interférence, et vous pouvez utiliser ces PDF pour créer des motifs d'œil. Nous avons également observé comment les réflexions créent du bruit de signal en regardant le PDF d'interférence s'élargir à mesure que nous prenions en compte les réflexions de la réponse à l'impulsion. Enfin, nous avons observé à quel point il devient extrêmement difficile d'atteindre une performance sans erreur d'un canal à mesure que la modulation augmente. J'espère que cela donne aux lecteurs une appréciation pour le besoin de réduire les réflexions et d'augmenter la technologie, comme l'ajout de FEC.
Jusqu'à la prochaine fois, restez en sécurité !
Les outils de conception dans Altium Designer® contiennent tout ce dont vous avez besoin pour suivre les nouvelles technologies. Parlez-nous aujourd'hui et découvrez comment nous pouvons améliorer votre prochaine conception de PCB.