Your Complete Guide to Via Stub Analysis
Via stubs are sometimes viewed as an annoyance, especially when you only need to make a transition between adjacent layers. For low speed, less-dense boards with low layer count, via stubs are an afterthought, or they may not receive consideration at all. For faster edge rates/higher frequencies, the conventional wisdom is to remove all via stubs. The question is: what exactly counts as “high frequency,” and how do you figure out the relevant length?
To do this correctly, you’ll need to borrow a few tools from circuit theory to understand the electrical function of a via stub, and you’ll need to borrow some elements from transmission line theory. As it turns out, just like a regular trace on a PCB, an electrically long via stub will act like a transmission line. It gets more interesting when we consider what happens at high-GHz frequencies in a real PCB, where parasitics become problematic. So to properly understand via stubs, we have to look at them from two perspectives: using a circuit model and as an electrically long structure with propagating waves.
Via Stub as a Circuit Model
I’ll be one of the first people to tell you that circuit models are not exact for describing real designs. Circuit models, especially RLC circuits, are very useful as a language that can describe electrical behavior, but circuit models should not be taken literally. That being said, we can still intuitively create a circuit model describing via stubs by looking at the structure of a via, any nearby conductors held at constant potential (power/ground planes), and the transmission line sections connected to it.
The image below shows a diagram of a typical via with its stub, nearby pads/planes, and some circuit elements to indicate the electrical behavior in different portions of the via/stub. The electrical behavior is dominated by the series inductance and resistance in the via and stub. However, there is also parasitic capacitance back to the other conductors, as shown with the capacitor symbols.

At Low Frequencies, No Stitching Vias
At low frequencies, the electrical description of a via is normally as an inductor with some non-zero DC resistance in series (thus the series inductor and resistor symbols in the above diagram). This means the impedance of the via, including the skin effect and copper roughness, would be:

In this equation, the copper roughness factor K basically increases the skin effect resistance and has a complicated spectrum; research on properly modeling copper roughness continues to be active. Basically, the via’s impedance can be modeled as inductive at sufficiently low frequencies. This equation is only an approximation, however, as the via impedance is in parallel with a distributed capacitance back to nearby conductors.
Real Via Impedance
The real description of a via's impedance depends on a few important factors, and these are generally totally ignored in via impedance and propagation calculators:
- Pad size
- Antipad size
- Stitching via arrangement
- Via hole diameter
At high frequencies, the capacitance becomes much more important and all via structures are sensitive to any nearby capacitive loading. The result is that the via's impedance could appear either capacitive or inductive at high frequencies. To learn more about this issue with designing vias, take a look at the following article to fully understand the factors determining via impedance.
Via Stubs as Transmission Line Sections
If you think about it briefly, it should be obvious how a via stub will act like a transmission line section in terms of its electrical behavior. Signals have a finite propagation speed along an interconnect, and this finite propagation speed is the basis for transmission line behavior in any electrical structure.
The image below shows how a via, its stub, and its input/output lines can be redefined in terms of the input impedance of transmission line sections. Note that the via stub and the main via body may not have the same ground reference as the input and output lines. In any case, the via and via stub will cause a propagating signal to see some input impedance looking into the transmission line sections.

The via stub is basically a short transmission line with an open circuit load. As such, a signal propagating through the via will see an input impedance at the boundary of the via stub defined by an open-circuit load; this is one reason the via stub length is generally limited below a quarter-wavelength of the propagating signal (note the definition of bandwidth here!).
In terms of transmission line theory, this is a complex problem that has an iterative solution; read this article from Khongdeach et al. to see the actual solution method. The input impedance at the end of line 1 is a function of the input impedance seen at the stub/line 2 connection. The goal in this problem is to determine the critical length for the stub such that the input impedance of the vis stub is extremely large (infinity). For this reason, everyone just plays it safe and says to remove all via stubs on high speed lines. Unfortunately, every hole that needs to be drilled in a board adds cost, so you need to choose which stubs should be backdrilled and which to ignore.
What is the Quarter-Wavelength Limit?
When a signal begins to propagate into a via stub, there will be specific frequencies that will experience strong loss due to destructive interference. The via stub is essentially an open transmission line, and a signal propagating into the stub will reflect off the open end. The result is that the reflected signal will interfere with the input signal. At certain frequencies, there will be destructive interference, and a deep peak will be seen in an insertion loss plot looking into the interconnect.
The lowest order frequency that will produce destructive interference occurs when the via length is equal to one-quarter of the wavelength corresponding to the input frequency. At this particular frequency, the wave will experience a 180˚ phase shift and will destructively interfere with the input signal. This causes the input and reflected signal to cancel, causing little power to reach the load at that particular frequency.
It is simple to derive an infinite set of frequencies producing theoretically infinite insertion loss by noticing that any odd multiple of a quarter wavelength will experience strong insertion loss in the via stub:
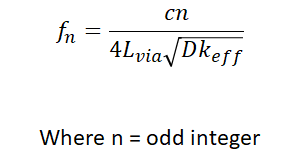
The challenge here is to calculate the Dk-effective value. For a single-ended via, this will be approximately equal to Dk, although it can be slightly higher due to the sizes of pads/antipads and due to the in-plane/out-of-plane Dk values for the laminate. Typically, the deviation will not be more than 10% according to field solver calculations.
For stubs on a pair of differential vias, there is a Dk-effective value that depends on the spacing and sizing of the two vias in the pair, as well as the antipad size. The geometric parameters and Dk-effective formula are:
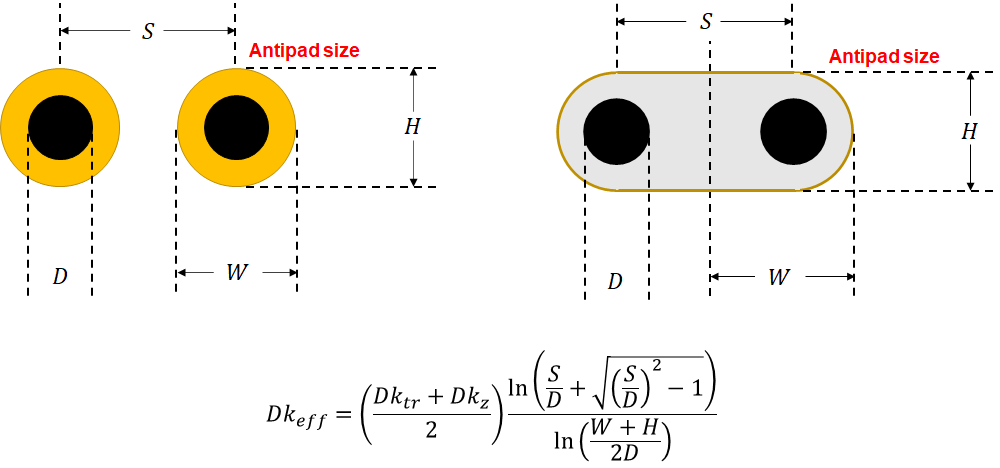
Here you need to know the in-plane (Dk-xy) and transverse (Dk-z) values of Dk for the laminate materials. Of course, most stackups are hybrids and will use multiple different weaves and resin contents, so the calculation of these various Dk values is difficult. The result is that, for a set of Dk ~ 4 substrate materials, you can expect Dk-effective ~ 10 as a rough approximation.
Quarter-Wavelengths Observable in S21 Spectra
An example insertion loss plot (S21) showing the occurrence of a quarter-wave anti-resonance in a single-ended via on a 10-layer board (2 mm thick, Dk = 4 in all layers) was computed using Simbeor. The stub on this via is 68 mil long and 4 stitching vias. The 3D model for this example is shown below.
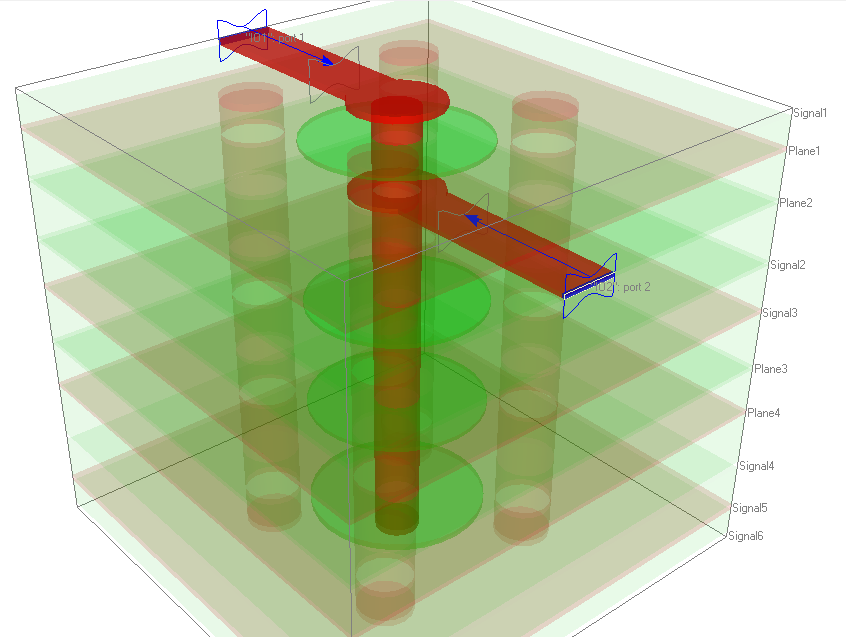
The plot below shows the insertion loss spectrum with strong losses clearly visible at approximately 22.3 GHz and 65.0 GHz (very close to the theoretical n = 3 value of 66.9 GHz). The loss in this via structure is strong enough to totally limit the bandwidth of this interconnect for digital signals to about 15 GHz. We would expect these dips to re-occur at odd multiples of the lowest order frequency (i.e., 111.5 GHz, 156.1 GHz, and so on).

In RF systems, where interconnects are generally single-ended, this means a particular via can strongly suppress propagation at specific frequencies, even if the system is built with low-loss laminates and smooth conductors. The same idea applies to differential interconnects with digital signals, but this causes some of the power to be lost at certain frequencies, resulting in signal distortion.
Set a Via Stub Length Limit
The reality is that you don’t need to totally remove every via stub in your PCB, you just need to aim for a maximum stub length. This can be done in your stackup definition and in your design rules, including in Altium Designer. Remember, the quarter wavelength limit will define the frequency where we expect a high-Q antiresonance with very high insertion loss; we need to limit the useful bandwidth below that quarter wavelength frequency. This can be some fraction of the lowest-order via resonance, such as 50%. Let’s use this value in an example:
Bandwidth Limit Example
As a rough approximation, consider a single-ended signal with a typical 0.25 mm (10 mil) leftover stub tolerance. For a Dk = 4 stackup, we would have a lowest-order quarter-wavelength frequency of 150 GHz, or we could set a conservative 50% bandwidth limit, we would have a signal bandwidth of 75 GHz. If we consider the case where we have a differential pair, in a typical case with a substrate Dk of 4 and effective Dk of ~10, the bandwidth limit on a stub will be somewhat smaller. In this case, our 0.25 mm (10 mil) the stub will have a quarter-wavelength frequency of 95 GHz, or a 50% bandwidth limit of 47.5 GHz.
Stub Length ExampleA
If instead, for example, we want to ensure we would have at least a certain bandwidth, we could calculate a stub length. For example, suppose we want to ensure a single-ended signal has 50% bandwidth value of 28 GHz on a Dk = 3.7 substrate. This means our lowest order stub frequency is 56 GHz, and the stub length would be 27.9 mil.
For another in-depth example on stub analysis, take a look at this case study involving an Altium Designer example project and stubs on a PCIe Gen4 connector.
The values outlined above illustrate how even a short via stub of only 10 mils is sufficient for most high speed protocols and some commercial mmWave applications (e.g., radar or imaging). In single-ended signals operating well into mmWave frequencies, the typical approach is to use a blind via for the signal coming off of a connector or component, rather than use a through-hole and backdrill the stub. If you can’t use a blind via, the best strategy to avoid the need for backdrilling is to route across the stack and place the destination route closer to the opposite side of the board.
If you need to design high speed/high frequency boards with short or removed via stubs, the routing and layout tools in Altium Designer® make it easy to set limits on via stub lengths. You can define limits as design rules, include backdrilling instructions in your drill table and fabrication documents, and prepare all other deliverables for manufacturing.
When you’ve finished your design, and you want to share your project, the Altium 365™ platform makes it easy to collaborate with other designers. We have only scratched the surface of what is possible to do with Altium Designer on Altium 365. You can check the product page for a more in-depth feature description or one of the On-Demand Webinars.