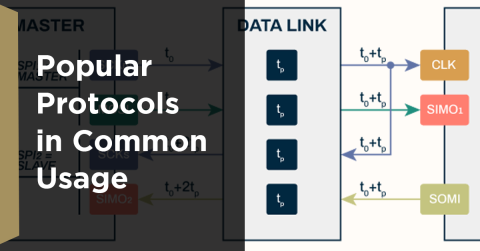
Data Rate vs Bandwidth: What's the Difference?

Data rate and bandwidth are sometimes used interchangeably, thanks largely to advertising firms and the media, who turned an important technical term from analog circuit design into a buzzword. The word “bandwidth” is now misused to the point where it has unintentionally taken on a somewhat related meaning from ADC design. In PCB design and circuit design, bandwidth sometimes has a clear distinction that has nothing to do with data rate, and sometimes it refers to some quality of the signal and its interaction with a receiver.

With the difference between data rate vs bandwidth being murky, how does it relate back to your PCB design? We’ll look at this deeper in this article so that we can see how to define signal integrity metrics for ultra-high speed channels. These same ideas around signal integrity metrics are reflected in the recent USB 4.0 standard and will become more important in newer high speed signaling standards.

Data Rate vs. Bandwidth

Data rate is exactly what it sounds like: the number of bits transmitted through a channel or by a component per unit of time. Data rate may also be written in baud rate (e.g., the number of symbols per second), which allows us to differentiate between binary and multilevel signaling schemes (see below). This is pretty simple; for a 2-level (binary) bitstream (e.g., NRZ), the baud rate is equal to the bit rate. For 4-level signals (e.g., PAM4), the baud rate is half the bit rate as two bits are transmitted per unit interval (UI).

Bandwidth is generally used by electronics designers of all stripes to refer to one or more of the following:

• -3 dB point. If you’re designing a filter, this is usually used to denote the frequency where the filter’s transfer function (magnitude) drops by 3 dB. 
• Frequency range where a component can receive/transmit. I’ve normally seen this used by other researchers working on integration or system design, where there is a need to match a new component/system to receive/transmit within a specific frequency range. 
• Signal’s frequency content. A broadband signal may have its frequency content spread across a large range of frequencies, and bandwidth defines the size of this spectrum. 
• A channel's operating frequency range. This is the range of frequencies where a channel can transmit with low loss.
• A channel’s data rate capacity. This definition arises because the data rate (really the baud rate) and operating frequency range are related. It can be used to describe, fiber links, wireless links, or copper links in telecom, and it is not exclusive to describing board-level interconnects.

The last three points are more important for the digital designer as this is where the relationship between bandwidth vs. data rate needs to be made clear for PCB designers. There is an important distinction here between signal bandwidth and channel bandwidth. These are not the same thing. The channel bandwidth is always finite, meaning a channel can only reliably transmit frequencies up to a certain value.

From the above table, we should see that channels always have limited bandwidth, while your signal could have infinite bandwidth (digital signals). Here the channel bandwidth and signal bandwidth come together when we work on high-speed digital designs. The important point to know about high-speed digital systems design is:

For digital signals, the bandwidth is infinite. It is sometimes stated that digital signals must have finite bandwidth, but this is incorrect, and it can be proven that a digital signal's bandwidth is infinite just using the definition of Fourier series for a trapezoidal wave. The reason for this confusion comes from the idea that infinite power would be required to source a perfect digital signal. However, this does not mean that a real digital signal must have finite bandwidth just because the power it contains is finite.

For analog signals, we sometimes don't care about the signal bandwidth unless we are using modulation with a carrier signal (e.g., Ethernet), or we’re working with pulses (such as in lidar) or chirped waveforms (such as FMCW radar). The bandwidth for an analog signal is quite small and can be seen directly on a spectrum analyzer trace or calculated by applying an FFT to a time-domain measurment. You can generally define the bandwidth as the range of frequencies that is cut off by the noise floor in your oscilloscope trace. The situation isn’t so simple for digital frequencies.

What is the Digital Signal Bandwidth

Here, when I refer to bandwidth, I’m referring to the frequency content that makes up a digital signal, or the signal bandwidth. Here again I want to stress the difference between signal bandwidth and channel bandwidth by stating that a high-speed PCB designer should focus on hitting a channel bandwidth target; the signal bandwidth is always infinite so it inevitably does not matter.

If, however, we want to define a channel bandwidth design target for an interconnect, such as a transmission line for very high speed links, we can come up with a few different definitions:

• 5th harmonic. This is a common, but arbitrary cutoff point for digital signal bandwidths. I say this is arbitrary because you could also use any other odd frequency greater than the 5th harmonic. This definition says the bandwidth is 2.5 times the baud rate. 
• Knee frequency. This particular frequency is normally approximated as 0.5/t_rise. In other words, it says the bandwidth is generally not related to the data rate, although a higher binary data rate will have a shorter rise time.
• Nyquist frequency. Assuming a receiver only samples a binary digital signal at a rate that is equal to the baud rate, then the Nyquist frequency would be equal to half the baud rate.

When do each of these definitions matter? Immediately, I will tell you that the 5th harmonic limit is totally arbitrary and has no mathematical justification. The other two definitions depend on which type of signaling format you are using (square wave vs. digitally modulated analog wave).

Regular Square Wave Signals

As much as I see digital designers start quoting knee frequency as some sort of signal bandwidth limit, that was never the intent and it says nothing specifically about the energy contained in the power spectrum at different frequencies. The knee frequency is derived by examining the response of an RC circuit to an input square wave. This is done because, in the simplest sense, the input interface in a digital receiver can be modeled as an RC circuit, and we can relate the rise time to some bandwidth contained in the arriving signal.

In this context, the knee frequency just tells you the signal bandwidth that needs to reach the receiver. If we allow for inductance, digital receivers are just 2-pole low-pass filters, and the minimum channel bandwidth is derived in terms of the rise time assuming that the receiver's response is critically damped. The channel bandwidth is measuring whether the receiver's response to the square wave input allows its capacitance to charge up to the desired logic level within some time window. If the channel does not have enough bandwidth, then the rise time might be too slow, so in theory the receiver may not read an input logic signal within a required time window.

However, this is not actually how capacitive digital receivers work when excited with a square wave. For example, I2C and SPI do not have strict lower rise time limits, and in real components, you could see a range of different values that are acceptable. Focus on what the interface needs to operate properly to determine the minimum allowed rise time to ensure latching to a logic signal, and then use that to determine the minimum required bandwidth. In most practical cases with a correctly designed transmission line running up to a few Gbps, your channel will have plenty of bandwidth for these signals.

How To Calculate Minimum Required Channel Bandwidth for Modulated Signals

If you're desinging a channel to ensure it can pass a digitally modulated signal, how can you ensure the channel provides enough bandwidth so that the digital signal can be read by the receiver? This requires knowing the minimum amount of bandwidth, which is going to be some -3 dB frequency (or the knee frequency), or it will be the Nyquist frequency. There is an important point here:

The other two definitions are irrelevant for these types of signals. The most common instance where this type of channel design is used is in Ethernet, which uses pulse-amplitude modulation (PAM) constellations. For example, 100Base-T4 uses PAM-3, while 1000Base-T uses PAM-5 and 10GBase-T uses Tomlinson-Harashima Precoded PAM-16.

To determine the minimum bandwidth a channel needs to transmit a given modulated bitstream with digital data rate D, we can use the Nyquist theorem outined below: 

To see how this works, we'll take a look at the common signaling formats used in very high speed serial links (56 Gbps and higher):

Minimum Channel Bandwidth for RZ/NRZ and PAM-4

Today, the fastest differential serial links are using three possible data formats with pulse-amplitude modulation:

• Return to zero (RZ)
• Non-return to zero (NRZ)
• 4-level pulse-amplitude modulation (PAM-4)

RZ and NRZ use 2 signal levels per unit interval, while PAM-4 uses 4 levels. We could keep extending this to higher signal level numbers, such as the PAM-8 channel shown below. Note that PAM-8 is not in use yet in the fastest serial channels, it is just shown as an example, but who knows if that will change in the future.

For these modulated multi-level signals, the Nyquist frequency is the only relevant design target for the minimum channel bandwidth. Here, the bandwidth (equal to the Nyquist frequency) can be defined as:

where N is the number of signal levels per baud and D is the bit rate. This conceptually matches the same idea invoked in Nyquist’s criterion as defined for an ADC, where the sampling rate matches the baud rate. The takeaway is: just because we say a channel’s bandwidth is X GHz, it doesn’t mean the data rate is limited to 2X GHz; the signaling standard matters too.

Once you understand the difference between data rates vs bandwidth, you can use the PCB design and layout tools in Altium Designer^® to create compliant interconnects. You’ll have a complete set of routing and layout features for high speed impedance controlled designs.

Altium Designer on Altium 365^® delivers an unprecedented amount of integration to the electronics industry until now relegated to the world of software development, allowing designers to work from home and reach unprecedented levels of efficiency.

We have only scratched the surface of what is possible to do with Altium Designer on Altium 365. You can check the product page for a more in-depth feature description or one of the On-Demand Webinars.