Decoupling Capacitor Optimization and Resources for Power Integrity

Probably every IC datasheet and application note I’ve read does a poor job of explaining decoupling capacitor selection. There are three things they all seem to agree on:

• IC datasheets and application notes seem to agree that you need decoupling capacitors (they don’t always say why)
• They seem to agree that you need exactly two or three of them per large IC with different values (they don’t always say why, or they explain it incorrectly)
• They seem to agree on the range of values (1 nF, 10 nF, and 100 nF are most common)

Until I needed to confront power integrity in designs with FPGAs and fast MPUs, I never really questioned this guideline. It seemed to work fine with slower digital components like MCUs and other ICs. Being an analog guy and working with RF systems, some aspects of signal integrity and power integrity are actually easier; you only need to worry about impedances at the frequency of interest, rather than over a broad bandwidth.

For digital systems requiring ultra-stable DC power (e.g., large, fast ICs needing 1.2 V supplies), you have to think about decoupling capacitor optimization throughout a broad frequency range. We usually define target impedance based on the expected transient current pull into the PDN. Decoupling capacitor optimization aims to keep PDN impedance and transient response within desired limits.

Optimizing Your Decoupling Capacitor Selection

When designing a decoupling network for a large IC, there are a few things to consider:

• Capacitor placement: This is one area where a lot of application notes fall short in that they don’t explain the importance of loop inductance between the capacitor network output and the power.ground pins on the target IC. We want to layout the decoupling network to minimize loop inductance.
• Capacitor values and self-resonance frequency: In a previous article, I outlined one method to size the required total decoupling capacitance to supply sufficient transient current on the PDN from a time-domain perspective. This is a decent place to start and get a good idea of the required total capacitance, but we also need to look at the effects in the frequency domain to fully understand self-resonance.
• Number of capacitors: How many decoupling capacitors should you use? Do they need to have the same values or different values? If you look at some reference designs, you’ll see dozens of capacitors used on the PDN, not just a single capacitor.

From a circuit model standpoint, decoupling capacitor optimization targets points 2 and 3, and you’ll need to balance the number of capacitors you use with the total capacitance required at a given self-resonant frequency. Analog SPICE simulations are great tools to help you design the impedance of a decoupling network. You can also take an analytical approach. I’ll outline both briefly for the following circuit with four decoupling capacitors.

Real Capacitor Models

To properly optimize decoupling capacitor selection, we need to start with a circuit model for a real capacitor as this will help us identify resonances that arise purely due to discrete components and their parasitics. Real capacitors have some equivalent series inductance (ESL) and equivalent series resistance (ESR). This is shown in the example schematic below, which includes 4 decoupling capacitors and a capacitive load with high input impedance.

The ESL and ESR values shown above are only approximations for these generic components, they aren’t meant to represent values for a specific capacitor. However, you can construct such a model yourself using information from the manufacturer product guide for your capacitors, or you can use spectrum analyzer measurements to build a model for an individual capacitor.

Using Circuit Models for Decoupling Capacitor Optimization

If you use the method I outlined in a previous article to determine the total capacitance required to damp a large transient current spike, you can start to divide up the total capacitance among a set of discrete capacitors. To get started, we need the real impedance of a single capacitor in the above model:

Multiple Identical Capacitors

Again, the above equation is only for a single capacitor. When we have multiple capacitors in parallel, we need to calculate the equivalent impedance of the parallel capacitor arrangement. Interestingly, if we have N identical capacitors in parallel, the impedance of the parallel arrangement is just the single capacitor impedance divided by N. In other words, even in the presence of ESL and ESR, placing multiple capacitors in parallel provides total capacitance of NC, but the self-resonance frequency won’t change:

This explains why we like to put multiple identical capacitors in parallel:

• Total equivalent capacitance increases
• Total equivalent impedance decreases
• Self-resonance frequency does not change

This is an important step in understanding the number of capacitors you might need; for a given required total capacitance and target impedance, you can get to lower impedance and higher capacitance by using multiple identical capacitors.

If instead, we were to use one large capacitor rather than many small identical capacitors, we would have one self-resonance at low frequency. This can be very undesirable for digital signals, which would see inductive impedance at high frequencies in such a situation, and would lead to large voltage swings when the IC switches.

Multiple Capacitors with Different Values

When different capacitors are used, we now have a complicated equation to solve for the resonance frequencies and the total equivalent capacitance. Suppose we want to follow the example shown above with 4 different capacitors, each with different self-resonant frequency measured in isolation. When we combine these together in a circuit and try to calculate the impedance, we now have a polynomial of degree 2N to solve for the self-resonances (or 8th degree polynomial in the case of N = 4).

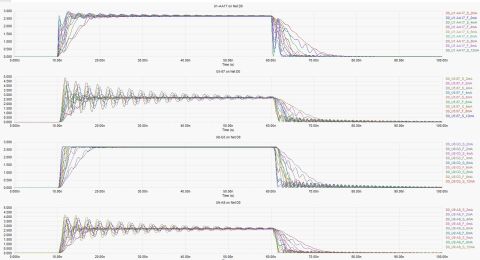
This is where analog simulations are useful because they can be used to calculate the resonances and equivalent impedance without having to solve such a complicated equation directly. The image below shows the impedance of the network shown in the above schematic using 4 capacitors, and using 5 of each type of capacitor (20 total).

Here, we gain some more insights:

• Adding more of each type of capacitor increases the total capacitance from that specific bank of capacitors, which reduces the peak impedance associated with that one capacitor. For example, if we want to reduce the peak at 197 MHz, we should add more of capacitor C4.
• Adding a new capacitor with different C or ESL values will create 1 or 2 new peaks in the PDN impedance spectrum.

Hopefully this explains how some boards can have an obscenely large number of small SMD caps simply for decoupling. Here, we still haven’t considered plane capacitance, which will give additional decoupling.

Add in the Plane Capacitance

Once you’ve determined the arrangement of discrete capacitors, the plane capacitance will be added in parallel to your decoupling network. The situation shown above is an idealization that accounts for a single portion of a decoupling network with a specific transient current response, so it’s good for dealing with one component. However, adding in the plane capacitance to the PDN impedance model only helps decrease the PDN impedance below the target value. If you like, you can simulate the network again with your estimated plane capacitance. Once your layout is finished, you can export your board into a field solver utility for a final design evaluation before prototyping.

When you need decoupling capacitor optimization in your board, the schematic design and mixed-signal simulation tools in Altium Designer® can help you determine the best capacitor values for your PDN. The updated simulation UI in Altium Designer 21 helps you build and analyze real capacitor models from generic components and use these in mixed-signal simulations.

When you’ve finished your design, and you want to share your project, the Altium 365™ platform makes it easy to collaborate with other designers. We have only scratched the surface of what is possible to do with Altium Designer on Altium 365. You can check the product page for a more in-depth feature description or one of the On-Demand Webinars.