What Causes Gibbs Signal Ringing in High-speed Channel Simulations?
Designing high speed channels on complex boards requires simulations, measurements on test boards, or both to ensure the design operates as you intend. Simulations can be used to generate predictions of signal behavior given a known input stimulus (pulse, bit sequence, or arbitrary waveform) using transforms and convolution operations. Unfortunately, it’s possible a simulation predicts behavior that doesn’t occur in reality due to incomplete models being used to describe a channel response.
Gibbs ringing is one of these effects that can occur when calculating a channel’s response using band-limited network parameters. When I write “band-limited” network parameters, I mean that the S-parameters for the channel do not have data that extends out to infinite frequency. Unfortunately, no measured S-parameters (or any other network parameters) will ever have infinite frequency content. Simple components (passives, lossless transmission lines, and some perfect RF circuits) can have perfectly known S-parameters out to infinite frequency, but real components and elements on your PCB will never be known with perfect accuracy.
Since all measured network parameter data you would use in a simulation is imperfect, what is the intrepid signal integrity engineer to do when creating channel response simulations? First, let’s look at the channel simulation process, as well as how parameters can be gently modified to suppress ringing artifacts and reveal true channel responses.
The Band-limited Channel Simulation Process
Just as is the case in measurements, Gibbs ringing can occur in channel simulations due to the fact that network parameters are typically band-limited.
- Network parameters for each element in a channel are calculated, procured from component manufacturers, or compiled from measurements
- The channel is constructed as a cascaded network and used to define a transfer function for the channel
- The transfer function is converter to an impulse response function using an inverse Fourier transform
- The convolution of the channel’s impulse response function and an input time-domain pulse is calculated; this gives the channel response to the desired input
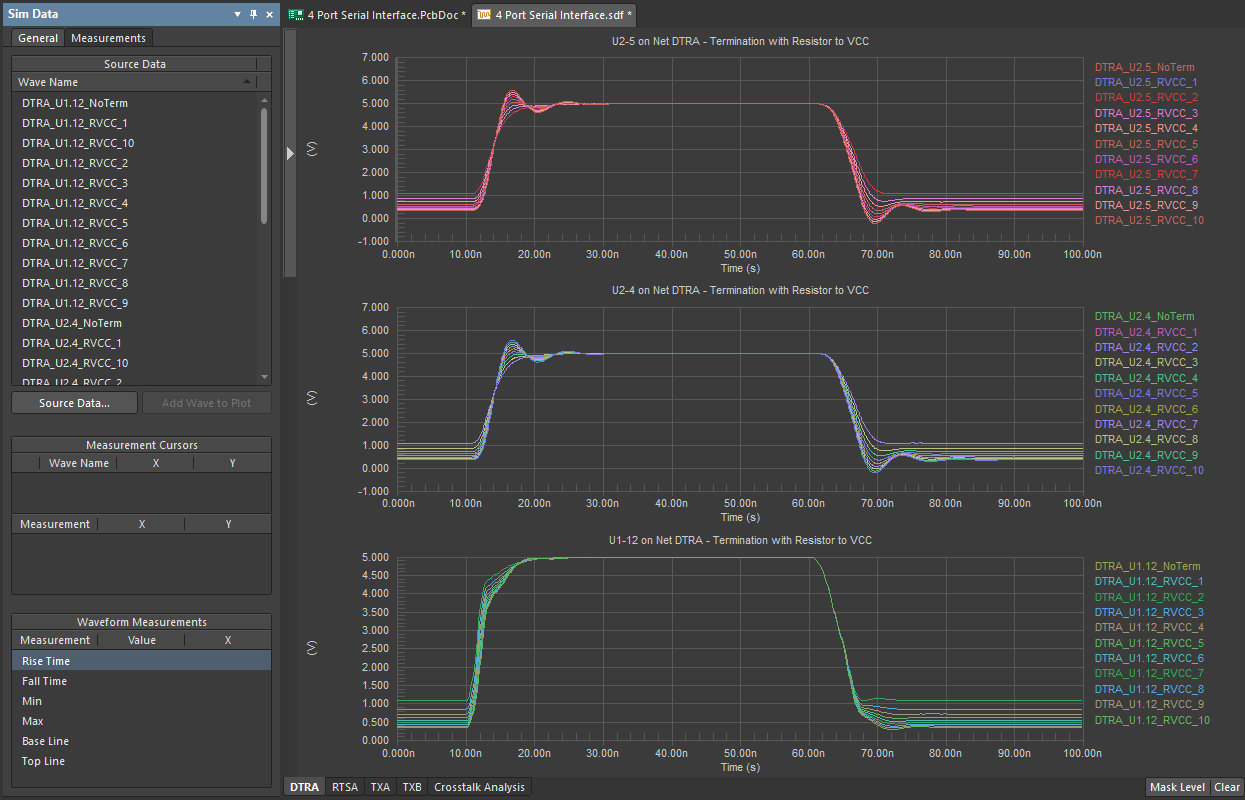
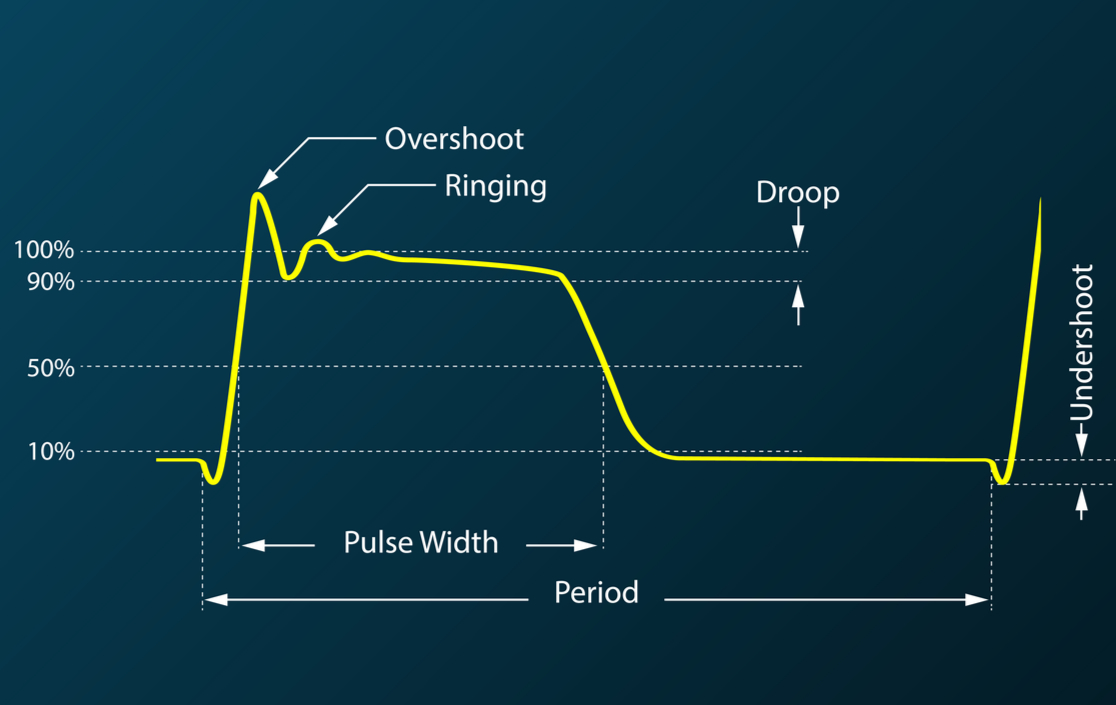
This process produces the channel response’s (i.e., output waveform) for an arbitrary input signal. Unfortunately, if there is an incorrectly-paired channel network parameter matrix and input signal, the calculated result will not be completely accurate and may contain Gibbs ringing. In other words, an impedance matched transmission line or circuit may appear to be mismatched within the frequency band of interest. This is the calculated analogue of the measurement problem identified in the previous article and is shown schematically below.

Now one has to ask, is the observed ringing real, or is it an artifact to be ignored? Note that there are real causes of ringing in circuits and channels, most commonly when there is nonlinear positive feedback or excess inductance. The above result may occur if the network parameters used in the simulation are bandlimited, i.e., data only exists out to sufficiently high frequencies.
The problem with using network parameter data (including S-parameters gathered from VNA measurements) to predict an arbitrary channel response is that the data is always bandlimited; it cannot be used to predict the design’s response to every possible input signal. When you’re designing a channel with cascaded elements, the channel’s bandwidth will always be limited by the element with the least bandwidth. This is because bandwidths add in parallel, as shown below:

Your job as the signal integrity engineer is to ensure the input signal is chosen so that its bandwidth does not exceed the bandwidth of the DUT network parameters (S-parameters are shown above). This means your digital signal and pulse cannot have too fast of a rising edge, otherwise you might predict a response that doesn’t exist.
Network Parameter Bandwidth
Just like your oscilloscope needs to have enough frequency-domain bandwidth to reconstruct a measured time-domain signal without sinc interpolation errors or band-limited transform errors, your network parameters also need to have sufficiently high bandwidth. This begs the question, what’s the minimum amount of bandwidth you need to resolve a given digital signal with known 10-90 rise time?
This is an important question because it relates to the filtering order of the channel or circuit you want to simulate. As I discussed in the previous article, and you can prove mathematically, all real transmission lines are fractional-order filters once dispersion and roughness are included; they are only first-order at low frequencies where roughness and skin resistance don’t matter. Other circuits, like a matching network and many printed RF circuits, can have inductive behavior and are 2nd or higher order filters. The filtering order of the channel will determine the amount of required bandwidth needed to resolve a digital signal with a defined rise time).
Thankfully there is a calculation you can use to determine the minimum required bandwidth for any general filter order with a defined -3 dB cutoff in the rolloff curve. This is quantified using the rise time-bandwidth product (literally the minimum bandwidth multiplied by 90-10 signal rise time). This is a bit complex and I won’t reproduce the results here (I’ll save it for another article). What you’ll find is that, up to very high order filters (at least 16th), the required bandwidth will be at minimum the inverse of the signal’s rise time.

This minimum bandwidth value required to resolve a signal with defined 10-90 rise time is a good rule of thumb for most 2-level digital signals.
Windowing
One trick you can use to apply a gentle rolloff in network parameters so that the system acts like a lower-order filter at high frequencies is to apply a window function. One reason we do this is because a lower-order filter requires less bandwidth than a higher order filter. Hamming and Tukey windows are common in processing MRI images, and both are appropriate for network parameter windowing. Jason Ellison’s discussion gives an excellent overview of various window functions; you can read his article at this link.
The other (simpler) trick is to just simulate the design with a slower signal. If your measurements are bandlimited, and you can’t go back and get new measurements out to higher frequencies, you can still get some idea of the channel response if you use a somewhat slower signal. You’ll still be able to see the transient response on the rising edge, but if the excitation waveform is at a sufficiently low bandwidth compared to the network parameters, you won’t see strong Gibbs ringing.
When you need to design, simulate, and layout your electronics while ensuring signal integrity and preventing the Gibbs phenomenon, use the complete set of PCB design, layout, and SPICE simulation features in Altium Designer®. When you need to extract network parameters from your interconnects and use these in simulations, you can use the EDB Exporter extension to import a design into Ansys field solvers and perform a range of SI/PI calculations. When you’ve finished your design, and you want to release files to your manufacturer, the Altium 365™ platform makes it easy to collaborate and share your projects.
We have only scratched the surface of what’s possible with Altium Designer on Altium 365. Start your free trial of Altium Designer + Altium 365 today.