Función de transferencia de filtro y análisis de polo-cero en Altium Designer

Recuerdo haber pasado horas en problemas de análisis de circuitos en mis clases de electrónica, y aprendí a analizar todo tipo de configuraciones de filtros/amplificadores a mano. Los circuitos generalmente eran tratables con la ley de Ohm y las leyes de Kirchoff, siempre y cuando no hubiera retroalimentación en el circuito. Los circuitos para aplicaciones avanzadas, como circuitos de adaptación de banda ancha o multibanda para componentes de RF, pueden volverse rápidamente difíciles de analizar a mano.

Pero a medida que el número de frecuencias resonantes en un filtro complejo supera las 2 o 3, el problema puede volverse rápidamente intratable. En este punto, el problema generalmente implica la descomposición o solución directa de un polinomio de 3er grado o superior, lo cual se vuelve inmanejable a mano. Incluso siendo un aficionado a las matemáticas, no soy fanático de los problemas de polinomios de grado superior. Afortunadamente, al tratar con filtros complejos, puedes determinar muchos aspectos del comportamiento de la señal

Análisis de un Circuito de Filtro Complejo

El circuito mostrado en el esquemático a continuación es un filtro bastante complejo. Aunque es posible que no te encuentres con este tipo de filtro en la práctica general, te acercarás bastante cuando estés diseñando un circuito de adaptación para una antena multibanda. En este circuito, la fuente (V2) envía una señal a un filtro de paso de banda, y la salida de esta parte (el voltaje a través del capacitor) se introduce en el filtro de rechazo de banda. El voltaje de salida del filtro se mide a través de L3 y C3. Este circuito de filtro fue construido usando los componentes genéricos en la biblioteca Miscellaneous Devices.IntLib. La fuente sinusoidal (V2) se puede encontrar en la biblioteca Simulation Sources.IntLib.

Un análisis simple de este filtro diría que hay dos polos importantes; un pico en el voltaje de salida en la frecuencia de resonancia RLC de paso de banda, y un cero en el voltaje de salida en la frecuencia de resonancia de rechazo de banda. En realidad, esto no es correcto. Esto se debe a que el capacitor C1 y el inductor L1 también participan en la resonancia con la parte de rechazo de banda de este circuito, creando una estructura de resonancia complicada en la función de transferencia del circuito.

Como veremos, hay más de dos picos y ceros en la función de transferencia del filtro. Esto se hace normalmente convirtiendo el circuito y la señal de entrada al dominio de Laplace. En general, la función de transferencia se puede escribir como una fracción de productos, como se muestra en la ecuación a continuación.

En esta ecuación, cada z es un cero en la función de transferencia, correspondiente a alguna frecuencia y tasa de decaimiento donde el circuito no permite pasar un voltaje de salida. Cada p es un polo, que corresponde a un pico en la función de transferencia. En circuitos lineales sin retroalimentación, los polos aparecerán en pares conjugados imaginarios o como pares conjugados complejos completos con parte real negativa. La parte real de un polo te indicará el comportamiento transitorio en el circuito.

Si intentas calcular las resonancias calculando los puntos críticos en el voltaje de salida, encontrarás que necesitas resolver un polinomio de sexto grado para determinar las frecuencias y así determinar los puntos críticos. Para el circuito anterior, aún tendrás que resolver un polinomio de sexto grado para determinar los polos en este circuito. Aunque este problema es técnicamente solucionable, es más rápido usar un simulador SPICE para determinar el comportamiento del circuito en el dominio de la frecuencia. En lugar de hacer este ejercicio a mano, resolveremos este problema con una simulación SPICE en Altium Designer.

Calculando la Función de Transferencia del Filtro

Para calcular la función de transferencia para este circuito, he colocado dos sondas (I y V) en la entrada y salida. La corriente de entrada solo experimentará cierta atenuación o amplificación cuando el circuito resuene en sus resonancias de paso de banda o de rechazo de banda. Una comparación de la medición del voltaje de salida (sonda V) se compara con el voltaje de entrada a una frecuencia específica para construir una función de transferencia (ver la ecuación anterior).

Para comenzar, abre el Panel de Simulación, y selecciona las fuentes y sondas de medición que se usarán en el análisis.

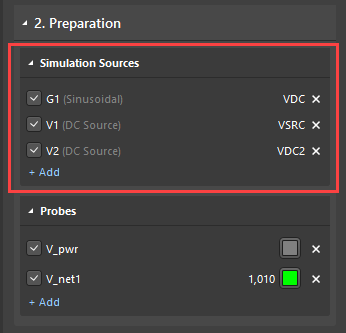
A continuación, habilita los siguientes análisis:

• Función de Transferencia: Seleccione un nombre de fuente y un nodo de referencia para usar en los cálculos de la función de transferencia en su red de circuitos.
• Análisis de Polo-Cero: Establezca el nodo de entrada en la red con R1 (NetR1_2) y el nodo de salida (NetC2_1). Asegúrese de dejar las opciones de nodo de referencia en “0”, ya que esto tomará mediciones de voltaje con respecto a tierra. Tenga en cuenta que, si hubiera un componente en algún lugar de la red conectado a tierra, entonces necesitaría cambiar estas opciones. Mis configuraciones se muestran en la imagen a continuación. Eche un vistazo a este artículo para obtener más información sobre cómo interpretar los resultados del análisis de polo-cero.

Las funciones de transferencia de filtros suelen mostrarse en un diagrama de Bode. Note que puede extraer la función de transferencia directamente, o puede extraer la función de transferencia compleja de un barrido en AC. Un diagrama de Bode es conveniente ya que muestra la magnitud y la fase de la función de transferencia en el dominio de frecuencia y en el estado estacionario (después de que todos los transitorios hayan decaído); esto le permite ver cómo el filtro afecta ambos aspectos importantes del comportamiento de la señal de entrada en un par de gráficos.

Análisis de los Resultados de su Función de Transferencia de Filtro

Una vez que hayas completado la configuración anterior, estarás listo para ejecutar tu simulación. Presiona F9 en el teclado o haz clic en Simular → Ejecutar Simulación. Verás una serie de gráficas en los resultados del barrido AC, y aparecerá una ventana separada que muestra los resultados del análisis de polos y ceros. El circuito de arriba contiene 6 polos y 2 ceros. Estos se muestran en la imagen a continuación. Ten en cuenta que las unidades en cada eje están en unidades de frecuencia angular (rad/s). Si quieres examinar el comportamiento en los resultados del barrido AC, entonces necesitas convertir a valores de frecuencia.

Dos de los polos se encuentran a lo largo de la porción negativa del eje real (es decir, no tienen parte imaginaria). Estos valores muestran que puedes obtener una salida momentánea del circuito cuando se alimenta con una función escalón o impulso. Sin embargo, la salida decaerá rápidamente con dos tasas de decaimiento exponencial superpuestas. Los otros polos y los dos ceros corresponden a frecuencias específicas, cuyo comportamiento se puede ver en los resultados del barrido AC.

Las gráficas a continuación muestran el comportamiento de este circuito en el dominio de la frecuencia. El cero a 1.453 MHz y los polos a 800.7 kHz y 2.885 MHz son claramente visibles en el diagrama de Bode (curva azul en la gráfica superior). La gráfica inferior muestra la fase de la función de transferencia, sin embargo, los ceros no se pueden ver en la gráfica del voltaje de salida (superpuesta en la gráfica superior, curva morada). La gráfica del voltaje de salida muestra que los polos 3 y 4 tienen una ganancia de ~2.3, y los polos 5 y 6 una ganancia de ~6.

Más con Análisis Transitorio

Si quieres profundizar más en esta simulación, puedes configurar la frecuencia de entrada a cualquiera de los valores de los polos mostrados en el diagrama de Bode y realizar un análisis transitorio. Este circuito muestra un comportamiento transitorio interesante debido al complejo comportamiento resonante de las dos partes de este circuito de filtro.

También puede ver cómo las respuestas transitorias en la corriente de entrada y el voltaje/potencia entregados al capacitor difieren a lo largo del tiempo. A continuación, se muestra un ejemplo. Un punto importante a recordar aquí es que este es un circuito LTI: la impedancia no varía en el tiempo, por lo que la respuesta transitoria que se observa aquí es un comportamiento estándar en un sistema lineal. A partir de esta gráfica, vemos que el voltaje (y la potencia reactiva) entregado a la carga capacitiva aumentará lentamente debido a la naturaleza reactiva general de este circuito de filtro. Ciertamente podríamos mirar otros voltajes/corrientes en diferentes puntos del circuito para ver cómo ocurre este comportamiento inicial de aumento en la corriente de entrada. Dejaré esto como un ejercicio para el lector.

Las herramientas de análisis previo al diseño en Altium Designer® te permiten hacer más que solo analizar funciones de transferencia de filtro para circuitos lineales. Puedes examinar la inmunidad al ruido, el comportamiento transitorio, los efectos de la temperatura en tus circuitos, y mucho más. Luego puedes capturar tu esquemático como un diseño inicial y diseñar todos los aspectos de tu próximo PCB. También tendrás un conjunto completo de herramientas para documentar todos los aspectos de tu proyecto, gestionar tu cadena de suministro y preparar los entregables para tu fabricante.

Ahora puedes descargar una prueba gratuita de Altium Designer y aprender más sobre las mejores herramientas de diseño de layout, simulación y planificación de producción de la industria. Habla hoy con un experto de Altium para saber más.