Analiza funkcji przenoszenia filtrów i analiza biegunów i zer w Altium Designer

Pamiętam, jak spędzałem godziny na zadaniach z analizy obwodów na zajęciach z elektroniki i nauczyłem się analizować wszelkiego rodzaju konfiguracje filtrów/wzmacniaczy ręcznie. Obwody zazwyczaj dawały się rozwiązać przy użyciu prawa Ohma i praw Kirchhoffa, o ile w obwodzie nie było sprzężenia zwrotnego. Obwody dla zaawansowanych zastosowań, takie jak szerokopasmowe lub wielopasmowe obwody dopasowujące dla komponentów RF, mogą szybko stać się trudne do analizy ręcznej.

Jednak gdy liczba częstotliwości rezonansowych w złożonym filtrze przekracza 2 lub 3, problem może szybko stać się nie do opanowania. W tym momencie problem zazwyczaj obejmuje dekompozycję lub bezpośrednie rozwiązanie wielomianu stopnia 3 lub wyższego, co staje się nie do zarządzania ręcznie. Nawet jako matematyk, nie przepadam za problemami z wielomianami wyższych stopni. Na szczęście, podczas zajmowania się złożonymi filtrami, można określić wiele aspektów zachowania sygnału

Analizowanie złożonego obwodu filtrującego

Układ przedstawiony na poniższym schemacie to dość skomplikowany filtr. Chociaż możesz się z tym typem filtra nie spotkać w ogólnej praktyce, będziesz do niego bardzo blisko, gdy będziesz projektować dopasowujący układ dla anteny wielopasmowej. W tym układzie, źródło (V2) wysyła sygnał do filtra pasmowoprzepustowego, a wyjście z tej części (napięcie na kondensatorze) jest wprowadzane do filtra pasmowozaporowego. Napięcie wyjściowe z filtra jest mierzone na L3 i C3. Ten układ filtru został zbudowany przy użyciu generycznych komponentów z biblioteki Miscellaneous Devices.IntLib. Sinusoidalne źródło (V2) można znaleźć w bibliotece Simulation Sources.IntLib.

Prosta analiza tego filtra wskazywałaby, że istnieją dwa ważne bieguny; szczyt napięcia wyjściowego przy częstotliwości rezonansowej RLC filtra pasmowoprzepustowego oraz zero napięcia wyjściowego przy częstotliwości rezonansowej filtra pasmowozaporowego. W rzeczywistości nie jest to prawidłowe. Dzieje się tak, ponieważ kondensator C1 i cewka L1 również uczestniczą w rezonansie z częścią pasmowozaporową tego układu, tworząc skomplikowaną strukturę rezonansową w funkcji przenoszenia układu.

Jak zobaczymy, w funkcji przenoszenia filtru występuje więcej niż dwa maksima i zera. Zazwyczaj osiąga się to poprzez przekształcenie obwodu i sygnału wejściowego do dziedziny Laplace'a. Ogólnie rzecz biorąc, funkcję przenoszenia można zapisać jako ułamek iloczynów, jak pokazano w poniższym równaniu.

W tym równaniu każde z jest zerem w funkcji przenoszenia, odpowiadającym pewnej częstotliwości i tempu zaniku, gdzie obwód nie pozwala na przepuszczenie napięcia wyjściowego. Każde p jest biegunem, który odpowiada maksimum w funkcji przenoszenia. W liniowych obwodach bez sprzężenia zwrotnego, bieguny pojawią się w parach sprzężonych zespolonych lub jako pełne pary sprzężone zespolone z ujemną częścią rzeczywistą. Rzeczywista część bieguna wskaże Ci zachowanie przejściowe w obwodzie.

Jeśli spróbujesz obliczyć rezonanse, obliczając krytyczne punkty w napięciu wyjściowym, odkryjesz, że musisz rozwiązać wielomian szóstego stopnia dla częstotliwości, aby określić punkty krytyczne. Dla powyższego obwodu nadal będziesz musiał rozwiązać wielomian szóstego stopnia, aby określić bieguny w tym obwodzie. Chociaż technicznie jest to problem rozwiązywalny, szybciej jest użyć symulatora SPICE, aby określić zachowanie obwodu w dziedzinie częstotliwości. Zamiast wykonywać to ćwiczenie ręcznie, rozwiążemy ten problem za pomocą symulacji SPICE w Altium Designer.

Obliczanie funkcji przenoszenia filtra

Aby obliczyć funkcję przenoszenia dla tego obwodu, umieściłem dwie sondy (I i V) na wejściu i wyjściu. Prąd wejściowy będzie po prostu doświadczał pewnego tłumienia lub wzmacniania, kiedykolwiek obwód rezonuje przy jego rezonansach pasmowoprzepustowych lub pasmowozaporowych. Porównanie pomiaru napięcia wyjściowego (sonda V) jest porównywane z napięciem wejściowym przy określonej częstotliwości, aby skonstruować funkcję przenoszenia (patrz powyższe równanie).

Aby rozpocząć, otwórz pulpit nawigacyjny symulacji i wybierz źródła oraz sondy pomiarowe, które będą używane w analizie.

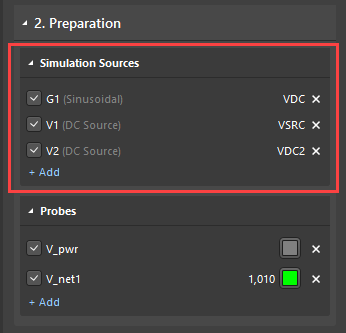
Następnie włącz następujące analizy:

• Funkcja Przenoszenia: Wybierz nazwę źródła i węzeł odniesienia, które będą używane do obliczeń funkcji przenoszenia w twojej sieci obwodów.
• Analiza Biegunów i Zer: Ustaw węzeł wejściowy na sieć z R1 (NetR1_2) oraz węzeł wyjściowy (NetC2_1). Upewnij się, że opcje węzła odniesienia są ustawione na „0”, ponieważ będzie to oznaczało pomiar napięcia względem ziemi. Zauważ, że gdyby na sieci był komponent połączony z ziemią, musiałbyś zmienić te opcje. Moje ustawienia są pokazane na poniższym obrazie. Zapoznaj się z tym artykułem, aby uzyskać więcej informacji na temat interpretacji wyników analizy biegunów i zer.

Funkcje przenoszenia filtrów są zazwyczaj pokazywane na wykresie Bodego. Zauważ, że możesz wyodrębnić funkcję przenoszenia bezpośrednio, lub możesz wyodrębnić złożoną funkcję przenoszenia z pomiaru AC. Wykres Bodego jest wygodny, ponieważ pokazuje wielkość i fazę funkcji przenoszenia w dziedzinie częstotliwości oraz w stanie ustalonym (po zaniku wszystkich przejściowych); pozwala to zobaczyć, jak filtr wpływa na oba ważne aspekty zachowania sygnału wejściowego na parze wykresów.

Analizowanie Wyników Funkcji Przenoszenia Twojego Filtra

Po zakończeniu powyższej konfiguracji, jesteś gotowy do uruchomienia symulacji. Naciśnij F9 na klawiaturze lub kliknij Symuluj → Uruchom symulację. Zobaczysz szereg wykresów w wynikach przesiewu AC, a w oddzielnym oknie pojawią się wyniki analizy biegun-zero. Układ powyżej zawiera 6 biegunów i 2 zera. Są one pokazane na poniższym obrazie. Zwróć uwagę, że jednostki na każdej osi są w jednostkach częstotliwości kątowej (rad/s). Jeśli chcesz zbadać zachowanie w wynikach przesiewu AC, musisz przekonwertować na wartości częstotliwości.

Dwa z biegunów leżą wzdłuż ujemnej części osi rzeczywistej (tj. nie mają części urojonej). Te wartości pokazują, że możesz uzyskać chwilowe wyjście z układu podczas zasilania funkcją skokową lub impulsową. Jednakże, wyjście to szybko zaniknie z dwoma nakładającymi się tempami zaniku wykładniczego. Pozostałe bieguny i dwa zera odpowiadają określonym częstotliwościom, których zachowanie można zobaczyć w wynikach przesiewu AC.

Poniższe wykresy pokazują zachowanie tego obwodu w dziedzinie częstotliwości. Zero przy 1,453 MHz oraz bieguny przy 800,7 kHz i 2,885 MHz są wyraźnie widoczne na wykresie Bodego (niebieska krzywa na górnym wykresie). Dolny wykres pokazuje fazę funkcji przenoszenia, jednak zera nie są widoczne na wykresie napięcia wyjściowego (nałożone na górnym wykresie, fioletowa krzywa). Wykres napięcia wyjściowego pokazuje, że bieguny 3 i 4 mają wzmocnienie około 2,3, a bieguny 5 i 6 mają wzmocnienie około 6.

Więcej z analizą przejściową

Jeśli chcesz posunąć się dalej z tą symulacją, możesz ustawić częstotliwość wejściową na dowolną z wartości dla biegunów pokazanych na wykresie Bodego i przeprowadzić analizę przejściową. Ten obwód wykazuje pewne interesujące zachowanie przejściowe ze względu na złożone zachowanie rezonansowe dla dwóch części tego obwodu filtrującego.

Możesz również zobaczyć, jak zmieniają się w czasie odpowiedzi przejściowe prądu wejściowego oraz napięcia/mocy dostarczanej do kondensatora. Poniżej przedstawiono przykład. Ważnym punktem do zapamiętania jest to, że jest to obwód LTI: impedancja nie zmienia się w czasie, więc obserwowana tutaj odpowiedź przejściowa jest standardowym zachowaniem w systemie liniowym. Z tego wykresu widzimy, że napięcie (i moc bierna) dostarczane do obciążenia pojemnościowego będzie powoli wzrastać ze względu na ogólnie bierny charakter tego obwodu filtrującego. Z pewnością moglibyśmy przyjrzeć się innym napięciom/prądom w różnych punktach obwodu, aby zobaczyć, jak zachodzi to początkowe wzrostowe zachowanie prądu wejściowego. Zostawię to jako ćwiczenie dla czytelnika.

Narzędzia do analizy przed układaniem w Altium Designer® pozwalają robić więcej niż tylko analizować funkcje przenoszenia filtrów dla obwodów liniowych. Możesz badać odporność na zakłócenia, zachowanie przejściowe, wpływ temperatury na twoje obwody i wiele więcej. Następnie możesz przechwycić swój schemat jako wstępny układ i zaprojektować wszystkie aspekty swojej następnej PCB. Będziesz miał również kompletny zestaw narzędzi do dokumentowania wszystkich aspektów twojego projektu, zarządzania łańcuchem dostaw i przygotowywania materiałów dla twojego producenta.

Teraz możesz pobrać darmową wersję próbną Altium Designer i dowiedzieć się więcej o najlepszych w branży narzędziach do projektowania układów, symulacji i planowania produkcji. Porozmawiaj z ekspertem Altium już dziś, aby dowiedzieć się więcej.