Função de Transferência de Filtro e Análise de Polo-Zero no Altium Designer

Lembro-me de passar horas em problemas de análise de circuitos nas minhas aulas de eletrônica, e aprendi a analisar todos os tipos de configurações de filtros/amplificadores manualmente. Os circuitos geralmente eram tratáveis com a lei de Ohm e as leis de Kirchoff, desde que não houvesse feedback no circuito. Circuitos para aplicações avançadas, como circuitos de correspondência de banda larga ou multibanda para componentes de RF, podem rapidamente se tornar difíceis de analisar manualmente.

Mas à medida que o número de frequências ressonantes em um filtro complexo excede 2 ou 3, o problema pode rapidamente se tornar intratável. Neste ponto, o problema geralmente envolve a decomposição ou solução direta de um polinômio de 3º grau ou superior, o que se torna inadministrável manualmente. Mesmo sendo bom em matemática, não sou fã de problemas com polinômios de grau superior. Felizmente, ao lidar com filtros complexos, você pode determinar muitos aspectos do comportamento do sinal

Analisando um Circuito de Filtro Complexo

O circuito mostrado no esquemático abaixo é um filtro bastante complexo. Embora você possa não encontrar este tipo de filtro na prática geral, você chegará bem perto quando estiver projetando um circuito de casamento para uma antena multibanda. Neste circuito, a fonte (V2) envia um sinal para um filtro passa-banda, e a saída desta parte (a tensão através do capacitor) é inserida no filtro rejeita-banda. A tensão de saída do filtro é medida através de L3 e C3. Este circuito de filtro foi construído usando os componentes genéricos na biblioteca Miscellaneous Devices.IntLib. A fonte senoidal (V2) pode ser encontrada na biblioteca Simulation Sources.IntLib.

Uma análise simples deste filtro diria que existem dois polos importantes; um pico na tensão de saída na frequência de ressonância RLC passa-banda, e um zero na tensão de saída na frequência de ressonância rejeita-banda. Na realidade, isso não é correto. Isso porque o capacitor C1 e o indutor L1 também participam na ressonância com a parte rejeita-banda deste circuito, criando uma estrutura de ressonância complicada na função de transferência do circuito.

Como veremos, existem mais de dois picos e zeros na função de transferência do filtro. Isso é normalmente feito convertendo o circuito e o sinal de entrada para o domínio de Laplace. Em geral, a função de transferência pode ser escrita como uma fração de produtos, conforme mostrado na equação abaixo.

Nesta equação, cada z é um zero na função de transferência, correspondendo a alguma frequência e taxa de decaimento onde o circuito não é permitido passar uma tensão de saída. Cada p é um polo, que corresponde a um pico na função de transferência. Em circuitos lineares sem feedback, os polos aparecerão em pares conjugados imaginários ou como pares conjugados complexos completos com parte real negativa. A parte real de um polo irá te dizer o comportamento transitório no circuito.

Se você tentar calcular as ressonâncias calculando os pontos críticos na tensão de saída, descobrirá que precisa resolver um polinômio de sexto grau para as frequências para determinar os pontos críticos. Para o circuito acima, ainda será necessário resolver um polinômio de sexto grau para determinar os polos neste circuito. Embora este problema seja tecnicamente solucionável, é mais rápido usar um simulador SPICE para determinar o comportamento do circuito no domínio da frequência. Em vez de fazer esse exercício manualmente, resolveremos este problema com uma simulação SPICE no Altium Designer.

Calculando a Função de Transferência do Filtro

Para calcular a função de transferência para este circuito, coloquei duas sondas (I e V) na entrada e saída. A corrente de entrada apenas experimentará alguma atenuação ou amplificação sempre que o circuito ressoar em suas ressonâncias de passagem de banda ou de rejeição de banda. Uma comparação da medição da tensão de saída (sonda V) é comparada com a tensão de entrada em uma frequência específica para construir uma função de transferência (veja a equação acima).

Para começar, abra o Painel de Simulação, e selecione as fontes e sondas de medição a serem usadas na análise.

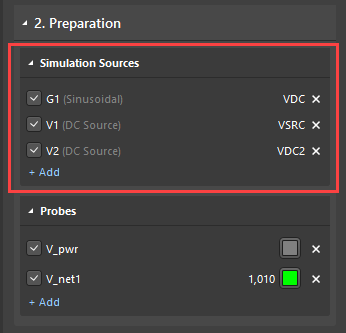
Em seguida, habilite as seguintes análises:

• Função de Transferência: Selecione um nome de fonte e um nó de referência para usar nos cálculos da função de transferência na sua rede de circuito.
• Análise de Polo-Zero: Defina o nó de entrada para a rede com R1 (NetR1_2) e o nó de saída (NetC2_1). Certifique-se de deixar as opções de nó de referência definidas como “0”, pois isso fará com que as medições de tensão sejam feitas em relação ao terra. Note que, se houvesse um componente em algum lugar na rede conectado ao terra, então você precisaria mudar essas opções. Minhas configurações são mostradas na imagem abaixo. Dê uma olhada neste artigo para mais informações sobre a interpretação dos resultados da análise de polo-zero.

As funções de transferência de filtros são geralmente mostradas em um gráfico de Bode. Note que você pode extrair a função de transferência diretamente, ou você pode extrair a função de transferência complexa a partir de uma varredura em AC. Um gráfico de Bode é conveniente, pois mostra a magnitude e a fase da função de transferência no domínio da frequência e no estado estacionário (após todos os transientes terem decaído); isso permite que você veja como o filtro afeta ambos os aspectos importantes do comportamento do sinal de entrada em um par de gráficos.

Analisando os Resultados da Função de Transferência do Seu Filtro

Uma vez que você tenha concluído a configuração acima, estará pronto para executar sua simulação. Pressione F9 no teclado ou clique em Simular → Executar Simulação. Você verá uma série de gráficos nos resultados da varredura AC, e uma janela separada aparecerá, mostrando os resultados da análise de polo-zero. O circuito acima contém 6 polos e 2 zeros. Estes são mostrados na imagem abaixo. Note que as unidades em cada eixo estão em unidades de frequência angular (rad/s). Se você quiser examinar o comportamento nos resultados da varredura AC, então você precisa converter para valores de frequência.

Dois dos polos estão localizados na parte negativa do eixo real (ou seja, eles não têm parte imaginária). Esses valores mostram que você pode obter uma saída momentânea do circuito quando alimentado com uma função degrau ou impulso. No entanto, a saída irá rapidamente decair com duas taxas de decaimento exponencial superpostas. Os outros polos e os dois zeros correspondem a frequências específicas, cujo comportamento pode ser visto nos resultados da varredura AC.

Os gráficos abaixo mostram o comportamento deste circuito no domínio da frequência. O zero em 1,453 MHz e os polos em 800,7 kHz e 2,885 MHz são claramente visíveis no gráfico de Bode (curva azul no gráfico superior). O gráfico inferior mostra a fase da função de transferência, no entanto, os zeros não podem ser vistos no gráfico da tensão de saída (sobreposto no gráfico superior, curva roxa). O gráfico da tensão de saída mostra que os polos 3 e 4 têm ganho de ~2,3, e os polos 5 e 6 têm ganho de ~6.

Mais Com Análise Transiente

Se você quiser avançar com esta simulação, pode definir a frequência de entrada para qualquer um dos valores dos polos mostrados no gráfico de Bode e executar uma análise transiente. Este circuito mostra um comportamento transiente interessante devido ao comportamento ressonante complexo para as duas partes deste circuito de filtro.

Você também pode ver como as respostas transientes na corrente de entrada e a tensão/potência entregue ao capacitor diferem ao longo do tempo. Um exemplo é mostrado abaixo. Um ponto importante a lembrar aqui é que este é um circuito LTI: a impedância não varia no tempo, então a resposta transiente vista aqui é um comportamento padrão em um sistema linear. A partir deste gráfico, vemos que a tensão (e a potência reativa) entregue à carga capacitiva aumentará lentamente devido à natureza reativa geral deste circuito de filtro. Certamente poderíamos olhar para outras tensões/correntes em diferentes pontos do circuito para ver como esse comportamento inicial de aumento na corrente de entrada ocorre. Deixarei isso como um exercício para o leitor.

As ferramentas de análise pré-layout no Altium Designer® permitem que você faça mais do que apenas analisar funções de transferência de filtro para circuitos lineares. Você pode examinar a imunidade a ruídos, comportamento transiente, efeitos da temperatura em seus circuitos e muito mais. Você pode então capturar seu esquemático como um layout inicial e projetar todos os aspectos de sua próxima PCB. Você também terá um conjunto completo de ferramentas para documentar todos os aspectos do seu projeto, gerenciar sua cadeia de suprimentos e preparar entregáveis para seu fabricante.

Agora você pode baixar uma versão de avaliação gratuita do Altium Designer e saber mais sobre as melhores ferramentas de layout, simulação e planejamento de produção do setor. Fale hoje mesmo com um especialista da Altium para saber mais.