Функция передачи фильтра и анализ нулей и полюсов в Altium Designer

Я помню, как проводил часы, решая задачи по анализу электрических цепей на занятиях по электронике, и научился вручную анализировать всевозможные конфигурации фильтров/усилителей. Цепи обычно поддавались расчету с помощью закона Ома и законов Кирхгофа, до тех пор, пока в цепи не появлялась обратная связь. Цепи для продвинутых приложений, такие как широкополосные или многополосные согласующие цепи для РЧ компонентов, могут быстро стать сложными для анализа вручную.

Но как только количество резонансных частот в сложном фильтре превышает 2 или 3, проблема может быстро стать неразрешимой. На этом этапе задача обычно включает в себя декомпозицию или прямое решение полинома 3-й степени или выше, что становится неуправляемым вручную. Даже будучи математиком, я не любитель задач с полиномами высших степеней. К счастью, при работе со сложными фильтрами, можно определить многие аспекты поведения сигнала

Анализ сложной фильтрующей цепи

На схеме ниже показан довольно сложный фильтр. Хотя вы можете не столкнуться с таким типом фильтра в общей практике, вы приблизитесь к этому, когда будете проектировать согласующую цепь для многодиапазонной антенны. В этой схеме источник (V2) посылает сигнал на полосовой фильтр, а выход с этой части (напряжение на конденсаторе) подается на полосно-заграждающий фильтр. Выходное напряжение с фильтра измеряется на L3 и C3. Эта схема фильтра была построена с использованием универсальных компонентов из библиотеки Miscellaneous Devices.IntLib. Синусоидальный источник (V2) можно найти в библиотеке Simulation Sources.IntLib.

Простой анализ этого фильтра показал бы, что есть две важные точки; пик выходного напряжения на резонансной частоте RLC полосового фильтра и ноль выходного напряжения на резонансной частоте полосно-заграждающего фильтра. На самом деле это не так. Это потому что конденсатор C1 и индуктор L1 также участвуют в резонансе с полосно-заграждающей частью этой схемы, создавая сложную структуру резонанса в передаточной функции схемы.

Как мы увидим, в передаточной функции фильтра присутствует более двух пиков и нулей. Обычно это достигается путем преобразования схемы и входного сигнала в область Лапласа. В общем случае передаточную функцию можно записать как дробь из произведений, как показано в уравнении ниже.

В этом уравнении каждый z является нулем в передаточной функции, соответствующим некоторой частоте и скорости затухания, где схема не пропускает выходное напряжение. Каждый p является полюсом, который соответствует пику в передаточной функции. В линейных схемах без обратной связи полюса появляются в виде пар комплексно-сопряженных чисел с мнимой частью или как полностью комплексно-сопряженные пары с отрицательной действительной частью. Действительная часть полюса скажет вам о переходном процессе в схеме.

Если вы попытаетесь вычислить резонансы, рассчитывая критические точки на выходном напряжении, вы обнаружите, что вам нужно решить полином шестой степени для определения частот, чтобы определить критические точки. Для приведенной выше схемы вам все равно придется решить полином шестой степени, чтобы определить полюса в этой схеме. Хотя эта проблема технически решаема, использование симулятора SPICE для определения поведения схемы в частотной области будет быстрее. Вместо того чтобы выполнять это упражнение вручную, мы решим эту проблему с помощью симуляции SPICE в Altium Designer.

Расчет функции передачи фильтра

Чтобы рассчитать функцию передачи для этой схемы, я разместил два датчика (I и V) на входе и выходе. Входной ток будет просто испытывать некоторое ослабление или усиление всякий раз, когда схема резонирует на ее полосовых или полосовых резонансах. Сравнение измерения выходного напряжения (датчик V) сравнивается с входным напряжением на определенной частоте для построения функции передачи (см. приведенное выше уравнение).

Чтобы начать, откройте панель управления симуляцией и выберите источники и измерительные датчики, которые будут использоваться в анализе.

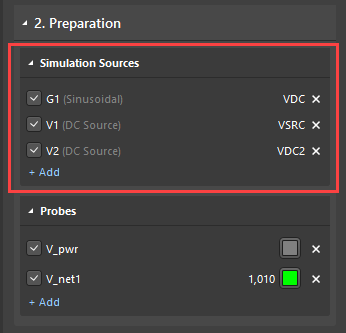
Затем включите следующие анализы:

• Передаточная функция: Выберите имя источника и узел отсчета для расчета передаточной функции в вашей сети схемы.
• Анализ нулей и полюсов: Установите входной узел на сеть с R1 (NetR1_2) и выходной узел (NetC2_1). Убедитесь, что опции узла отсчета установлены на “0”, так как это позволит производить измерения напряжения относительно земли. Обратите внимание, что если бы на сети был компонент, подключенный к земле, вам бы потребовалось изменить эти параметры. Мои настройки показаны на изображении ниже. Посмотрите эту статью для получения дополнительной информации о том, как интерпретировать результаты анализа нулей и полюсов.

Передаточные функции фильтров обычно показывают на диаграмме Боде. Обратите внимание, что вы можете извлечь передаточную функцию напрямую, или вы можете извлечь комплексную передаточную функцию из АЧХ. Диаграмма Боде удобна, так как она показывает величину и фазу передаточной функции в частотной области и в установившемся режиме (после затухания всех переходных процессов); это позволяет вам видеть, как фильтр влияет на оба важных аспекта поведения входного сигнала в паре графиков.

Анализ результатов передаточной функции вашего фильтра

После того, как вы завершили настройку выше, вы готовы запустить симуляцию. Нажмите F9 на клавиатуре или выберите Simulate → Run Simulation. Вы увидите ряд графиков в результате АЧХ, и появится отдельное окно, которое покажет результаты анализа полюсов и нулей. Приведенная выше схема содержит 6 полюсов и 2 нуля. Они показаны на изображении ниже. Обратите внимание, что единицы измерения на каждой оси указаны в единицах угловой частоты (рад/с). Если вы хотите изучить поведение в результате АЧХ, то вам нужно перевести значения в частоты.

Два из полюсов лежат вдоль отрицательной части вещественной оси (то есть, они не имеют мнимой части). Эти значения показывают, что вы можете получить мгновенный выходной сигнал от схемы при подаче ступенчатой функции или импульса. Однако выходной сигнал быстро угаснет с двумя наложенными экспоненциальными скоростями затухания. Остальные полюса и два нуля соответствуют определенным частотам, поведение которых можно увидеть в результате АЧХ.

На графиках ниже показано поведение данной схемы в частотной области. Ноль на частоте 1,453 МГц и полюса на частотах 800,7 кГц и 2,885 МГц четко видны на графике Боде (синяя кривая на верхнем графике). Нижний график показывает фазу передаточной функции, однако нули не видны на графике выходного напряжения (наложен на верхний график, фиолетовая кривая). График выходного напряжения показывает, что полюса 3 и 4 имеют усиление ~2,3, а полюса 5 и 6 - усиление ~6.

Больше с анализом переходных процессов

Если вы хотите углубиться в эту симуляцию, вы можете установить частоту входного сигнала равной любому из значений полюсов, показанных на графике Боде, и выполнить анализ переходных процессов. Эта схема демонстрирует некоторое интересное переходное поведение из-за сложного резонансного поведения для двух частей этой фильтрующей схемы.

Вы также можете увидеть, как изменяются во времени переходные процессы в токе на входе и напряжении/мощности, подаваемой на конденсатор. Пример показан ниже. Важно помнить, что это линейная цепь с постоянными параметрами (LTI-цепь): импеданс не изменяется со временем, поэтому наблюдаемый здесь переходный процесс является стандартным поведением в линейной системе. Из этого графика видно, что напряжение (и реактивная мощность), подаваемое на емкостную нагрузку, будет медленно увеличиваться из-за общего реактивного характера этой фильтрующей цепи. Мы могли бы, конечно, рассмотреть другие напряжения/токи в различных точках цепи, чтобы увидеть, как происходит это начальное увеличение тока на входе. Я оставлю это в качестве упражнения для читателя.

Инструменты предварительного анализа в Altium Designer® позволяют делать гораздо больше, чем просто анализировать функции передачи фильтров для линейных цепей. Вы можете изучать устойчивость к помехам, переходные процессы, температурные эффекты в ваших цепях и многое другое. Затем вы можете зафиксировать вашу схему как начальную компоновку и спроектировать все аспекты вашей следующей печатной платы. У вас также будет полный набор инструментов для документирования всех аспектов вашего проекта, управления цепочкой поставок и подготовки результатов для вашего производителя.

Теперь вы можете скачать бесплатную пробную версию Altium Designer и узнать больше о лучших в отрасли инструментах для разработки плат, моделирования и планирования производства. Обратитесь к эксперту Altium сегодня, чтобы узнать больше.