Altium Designerにおけるフィルタ伝達関数と極-零点解析

電子工学の授業で回路解析の問題に何時間も費やしたことを覚えています。手計算で様々なフィルター/アンプの構成を分析する方法を学びました。回路は通常、フィードバックがない限り、オームの法則やキルヒホッフの法則で扱えました。RFコンポーネント用の広帯域やマルチバンドマッチング回路など、高度なアプリケーションの回路は、手計算で分析するのがすぐに難しくなります。

しかし、複雑なフィルターの共振周波数の数が2または3を超えると、問題はすぐに扱いきれなくなります。この時点で、問題は通常、3次以上の多項式の分解または直接解を求めることになり、手計算では管理不可能になります。数学が得意な私でも、高次の多項式の問題は好きではありません。幸いなことに、複雑なフィルターを扱う際には、信号の挙動の多くの側面を決定できます

複雑なフィルター回路の解析

以下の回路図に示されている回路は、かなり複雑なフィルターです。一般的な実践でこのタイプのフィルターに遭遇することはないかもしれませんが、マルチバンドアンテナ用のマッチング回路を設計しているときには、かなり近いものになります。この回路では、ソース（V2）が信号をバンドパスフィルターに送り、この部分からの出力（キャパシタを通過する電圧）がバンドストップフィルターに入力されます。フィルターからの出力電圧はL3とC3を通過する電圧で測定されます。このフィルター回路は、Miscellaneous Devices.IntLibライブラリの汎用コンポーネントを使用して構築されました。正弦波源（V2）は、Simulation Sources.IntLibライブラリで見つけることができます。

このフィルターの簡単な分析では、2つの重要な極があると言えます。バンドパスRLC共振周波数での出力電圧のピークと、バンドストップ共振周波数での出力電圧のゼロです。しかし、実際にはこれは正しくありません。これは、キャパシタC1とインダクタL1もこの回路のバンドストップ部分と共振しており、回路の伝達関数に複雑な共振構造を作り出しているためです。

見ていくとわかるように、フィルター伝達関数には2つ以上のピークとゼロがあります。これは通常、回路と入力信号をラプラス領域に変換することによって行われます。一般に、伝達関数は以下の方程式に示されるように、積の分数として書くことができます。

この方程式では、各zは伝達関数のゼロであり、回路が出力電圧を通過させない特定の周波数と減衰率に対応しています。各pは極であり、伝達関数のピークに対応します。フィードバックのない線形回路では、極は虚数共役ペアまたは負の実部を持つ完全な複素共役ペアとして現れます。極の実部は、回路の過渡的な挙動を教えてくれます。

出力電圧の臨界点を計算することで共振を計算しようとすると、臨界点を決定するために6次の多項式を解く必要があることがわかります。上記の回路についても、この回路の極を決定するために6次の多項式を解く必要があります。この問題は技術的に解決可能ですが、周波数領域での回路の挙動を決定するためにSPICEシミュレータを使用する方が速いです。この演習を手作業で行う代わりに、Altium DesignerでSPICEシミュレーションを使用してこの問題を解決します。

フィルタ伝達関数の計算

この回路の伝達関数を計算するために、入力と出力に2つのプローブ（IとV）を配置しました。入力電流は、回路がそのバンドパスまたはバンドストップ共振で共振するたびに、いくつかの減衰または増幅を経験します。出力電圧測定（Vプローブ）の比較は、特定の周波数での入力電圧と比較して伝達関数を構築するために使用されます（上記の方程式を参照）。

始めるには、シミュレーションダッシュボードを開き、分析に使用するソースと測定プローブを選択します。

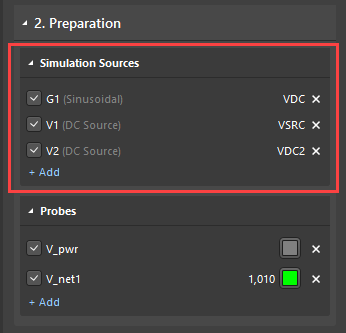
次に、以下の分析を有効にします：

• 伝達関数：伝達関数の計算に使用するソース名と基準ノードを選択してください。
• 極-零点解析：入力ノードをR1（NetR1_2）に接続されたネットに設定し、出力ノード（NetC2_1）を設定します。基準ノードオプションを「0」に設定したままにしてください。これは、基準を地面に対する電圧測定とするためです。ネット上のどこかに地面に接続されたコンポーネントがある場合は、これらのオプションを変更する必要があります。私の設定は下の画像に示されています。極-零点解析結果の解釈に関する詳細は、この記事をご覧ください。

フィルタ伝達関数は通常、ボード線図で示されます。伝達関数を直接抽出することも、ACスイープから複素伝達関数を抽出することもできます。ボード線図は便利です。なぜなら、周波数領域および定常状態（すべての過渡現象が減衰した後）で伝達関数の大きさと位相を示すからです。これにより、入力信号の挙動の両方の重要な側面がフィルタによってどのように影響されるかを一対のプロットで確認できます。

フィルタ伝達関数結果の分析

上記の設定を終えたら、シミュレーションを実行する準備が整います。キーボードのF9を押すか、Simulate → Run Simulationをクリックします。ACスイープの結果にはいくつかのプロットが表示され、ポール・ゼロ解析の結果を示す別ウィンドウが現れます。上記の回路には6つのポールと2つのゼロが含まれています。これらは下の画像に示されています。各軸の単位が角周波数（rad/s）であることに注意してください。ACスイープの結果で挙動を調べたい場合は、周波数値に変換する必要があります。

ポールのうち2つは実軸の負の部分に位置しています（つまり、虚数部分がありません）。これらの値は、ステップ関数やインパルスで回路から一時的な出力を得ることができることを示しています。しかし、出力は2つの重ね合わせた指数関数的減衰率で迅速に減衰します。他のポールと2つのゼロは特定の周波数に対応しており、その挙動はACスイープの結果で見ることができます。

以下のグラフは、この回路の周波数領域での振る舞いを示しています。ボード線図（上のグラフの青い曲線）で、1.453 MHzでのゼロ点と、800.7 kHzと2.885 MHzでの極がはっきりと見えます。下のグラフは伝達関数の位相を示していますが、出力電圧プロット（上のグラフに重ねてある紫の曲線）ではゼロ点は見えません。出力電圧グラフは、極3と4が約2.3のゲインを持ち、極5と6が約6のゲインを持つことを示しています。

過渡解析でさらに詳しく

このシミュレーションをさらに進めたい場合は、ボード線図に示された極のいずれかの値に入力周波数を設定し、過渡解析を実行できます。この回路は、このフィルタ回路の2つの部分に対する複雑な共振挙動のため、いくつかの興味深い過渡的な振る舞いを示します。

入力電流とコンデンサに供給される電圧/電力の過渡応答が時間とともにどのように異なるかも確認できます。以下に例を示します。ここで覚えておくべき重要な点は、これがLTI回路であることです：インピーダンスは時間とともに変化しないので、ここで見られる過渡応答は線形システムの標準的な振る舞いです。このプロットから、このフィルタ回路の全体的なリアクティブな性質により、コンデンサ負荷に供給される電圧（およびリアクティブ電力）が徐々に増加することがわかります。回路の異なる点での他の電圧/電流を見て、入力電流のこの初期の上昇挙動がどのように発生するかを確認することもできます。これは読者にとっての演習問題としておきます。

Altium Designer®のプリレイアウト分析ツールを使用すると、線形回路のフィルタ伝達関数を分析するだけでなく、ノイズ耐性、過渡挙動、回路の温度効果などを調べることができます。次に、初期レイアウトとして回路図をキャプチャし、次のPCBのすべての側面を設計できます。また、プロジェクトのすべての側面を文書化し、サプライチェーンを管理し、製造業者に提出する成果物を準備するための完全なツールセットも提供されます。

今なら、業界最高のレイアウト、シミュレーション、生産計画ツールについて学べる無料トライアル版のAltium Designerをダウンロードできます。本日、Altiumの専門家に相談して、さらに詳しく学びましょう。