Fonction de transfert de filtre et analyse pôle-zéro dans Altium Designer

Je me souviens avoir passé des heures sur des problèmes d'analyse de circuits dans mes cours d'électronique, et j'ai appris à analyser toutes sortes de configurations de filtres/amplificateurs à la main. Les circuits étaient généralement traitables avec la loi d'Ohm et les lois de Kirchoff, tant qu'il n'y avait pas de rétroaction dans le circuit. Les circuits pour des applications avancées, telles que les circuits d'adaptation large bande ou multibande pour les composants RF, peuvent rapidement devenir difficiles à analyser à la main.

Mais lorsque le nombre de fréquences de résonance dans un filtre complexe dépasse 2 ou 3, le problème peut rapidement devenir inextricable. À ce stade, le problème implique généralement la décomposition ou la résolution directe d'un polynôme de degré 3 ou supérieur, ce qui devient ingérable à la main. Même en tant que matheux, je ne suis pas fan des problèmes de polynômes de degré supérieur. Heureusement, lorsqu'on traite avec des filtres complexes, on peut déterminer de nombreux aspects du comportement du signal

Analyser un circuit de filtre complexe

Le circuit présenté dans le schéma ci-dessous est un filtre plutôt complexe. Bien que vous ne rencontriez peut-être pas ce type de filtre dans la pratique générale, vous vous en approcherez assez lorsque vous concevrez un circuit d'adaptation pour une antenne multibande. Dans ce circuit, la source (V2) envoie un signal dans un filtre passe-bande, et la sortie de cette partie (la tension aux bornes du condensateur) est entrée dans le filtre coupe-bande. La tension de sortie du filtre est mesurée aux bornes de L3 et C3. Ce circuit de filtre a été construit en utilisant les composants génériques de la bibliothèque Miscellaneous Devices.IntLib. La source sinusoïdale (V2) peut être trouvée dans la bibliothèque Simulation Sources.IntLib.

Une analyse simple de ce filtre dirait qu'il y a deux pôles importants ; un pic dans la tension de sortie à la fréquence de résonance RLC du passe-bande, et un zéro dans la tension de sortie à la fréquence de résonance du coupe-bande. En réalité, cela n'est pas correct. C'est parce que le condensateur C1 et l'inducteur L1 participent également à la résonance avec la partie coupe-bande de ce circuit, créant une structure de résonance compliquée dans la fonction de transfert du circuit.

Comme nous le verrons, il y a plus de deux pics et de zéros dans la fonction de transfert du filtre. Cela est normalement réalisé en convertissant le circuit et le signal d'entrée dans le domaine de Laplace. En général, la fonction de transfert peut être écrite comme une fraction de produits, comme le montre l'équation ci-dessous.

Dans cette équation, chaque z est un zéro dans la fonction de transfert, correspondant à une certaine fréquence et un taux de décroissance où le circuit n'est pas autorisé à passer une tension de sortie. Chaque p est un pôle, qui correspond à un pic dans la fonction de transfert. Dans les circuits linéaires sans rétroaction, les pôles apparaîtront en paires de conjugués imaginaires ou en paires de conjugués complexes complets avec une partie réelle négative. La partie réelle d'un pôle vous indiquera le comportement transitoire dans le circuit.

Si vous essayez de calculer les résonances en calculant les points critiques dans la tension de sortie, vous constaterez que vous devez résoudre un polynôme de sixième degré pour les fréquences afin de déterminer les points critiques. Pour le circuit ci-dessus, vous devrez toujours résoudre un polynôme de sixième degré pour déterminer les pôles de ce circuit. Bien que ce problème soit techniquement solvable, il est plus rapide d'utiliser un simulateur SPICE pour déterminer le comportement du circuit dans le domaine fréquentiel. Au lieu de faire cet exercice à la main, nous résoudrons ce problème avec une simulation SPICE dans Altium Designer.

Calcul de la fonction de transfert du filtre

Pour calculer la fonction de transfert pour ce circuit, j'ai placé deux sondes (I et V) à l'entrée et à la sortie. Le courant d'entrée ne fera que subir une atténuation ou une amplification chaque fois que le circuit résonne à ses résonances passe-bande ou coupe-bande. Une comparaison de la mesure de la tension de sortie (sonde V) est comparée à la tension d'entrée à une fréquence spécifique pour construire une fonction de transfert (voir l'équation ci-dessus).

Pour commencer, ouvrez le tableau de bord de simulation, et sélectionnez les sources et les sondes de mesure à utiliser dans l'analyse.

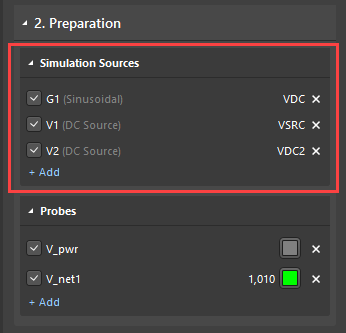
Ensuite, activez les analyses suivantes :

• Fonction de transfert : Sélectionnez un nom de source et un nœud de référence à utiliser pour les calculs de la fonction de transfert dans votre réseau de circuits.
• Analyse Pôle-Zéro : Définissez le nœud d'entrée sur le réseau avec R1 (NetR1_2) et le nœud de sortie (NetC2_1). Assurez-vous de laisser les options de nœud de référence sur “0”, car cela prendra les mesures de tension par rapport à la terre. Notez que, si un composant était connecté à la terre quelque part sur le réseau, alors vous devriez changer ces options. Mes paramètres sont montrés dans l'image ci-dessous. Jetez un œil à cet article pour plus d'informations sur l'interprétation des résultats de l'analyse pôle-zéro.

Les fonctions de transfert de filtre sont généralement représentées dans un diagramme de Bode. Notez que vous pouvez extraire la fonction de transfert directement, ou vous pouvez extraire la fonction de transfert complexe à partir d'un balayage en courant alternatif. Un diagramme de Bode est pratique car il montre l'amplitude et la phase de la fonction de transfert dans le domaine fréquentiel et en régime permanent (après que tous les transitoires se sont estompés) ; cela vous permet de voir comment le filtre affecte les deux aspects importants du comportement du signal d'entrée dans une paire de graphiques.

Analyse de vos résultats de fonction de transfert de filtre

Une fois que vous avez terminé la configuration ci-dessus, vous êtes prêt à lancer votre simulation. Appuyez sur F9 sur le clavier ou cliquez sur Simuler → Lancer la simulation. Vous verrez un certain nombre de graphiques dans les résultats du balayage AC, et une fenêtre séparée apparaîtra, qui montre les résultats de l'analyse des pôles et zéros. Le circuit ci-dessus contient 6 pôles et 2 zéros. Ceux-ci sont montrés dans l'image ci-dessous. Notez que les unités sur chaque axe sont en unités de fréquence angulaire (rad/s). Si vous souhaitez examiner le comportement dans les résultats du balayage AC, alors vous devez convertir en valeurs de fréquence.

Deux des pôles se trouvent le long de la portion négative de l'axe réel (c'est-à-dire, ils n'ont pas de partie imaginaire). Ces valeurs montrent que vous pouvez placer une sortie momentanée du circuit lors de l'alimentation avec une fonction d'échelon ou une impulsion. Cependant, la sortie décroîtra rapidement avec deux taux de décroissance exponentielle superposés. Les autres pôles et les deux zéros correspondent à des fréquences spécifiques, dont le comportement peut être observé dans les résultats du balayage AC.

Les graphiques ci-dessous montrent le comportement de ce circuit dans le domaine fréquentiel. Le zéro à 1,453 MHz et les pôles à 800,7 kHz et 2,885 MHz sont clairement visibles dans le tracé de Bode (courbe bleue dans le graphique supérieur). Le graphique inférieur montre la phase de la fonction de transfert, cependant, les zéros ne peuvent pas être vus dans le tracé de la tension de sortie (superposé dans le graphique supérieur, courbe violette). Le graphique de la tension de sortie montre que les pôles 3 et 4 ont un gain d'environ 2,3, et les pôles 5 et 6 un gain d'environ 6.

Plus avec l'analyse transitoire

Si vous souhaitez aller plus loin avec cette simulation, vous pouvez régler la fréquence d'entrée sur l'une des valeurs des pôles montrées dans le tracé de Bode et exécuter une analyse transitoire. Ce circuit montre un comportement transitoire intéressant en raison du comportement résonant complexe pour les deux parties de ce circuit de filtrage.

Vous pouvez également voir comment les réponses transitoires dans le courant d'entrée et la tension/puissance délivrée au condensateur diffèrent au fil du temps. Un exemple est montré ci-dessous. Un point important à retenir ici est que ceci est un circuit LTI : l'impédance ne varie pas dans le temps, donc la réponse transitoire vue ici est un comportement standard dans un système linéaire. À partir de ce graphique, nous voyons que la tension (et la puissance réactive) délivrée à la charge capacitive augmentera lentement en raison de la nature réactive globale de ce circuit de filtrage. Nous pourrions certainement examiner d'autres tensions/courants à différents points du circuit pour voir comment ce comportement initial de montée dans le courant d'entrée se produit. Je laisserai cela comme un exercice pour le lecteur.

Les outils d'analyse pré-layout dans Altium Designer® vous permettent de faire plus que simplement analyser les fonctions de transfert de filtre pour les circuits linéaires. Vous pouvez examiner l'immunité au bruit, le comportement transitoire, les effets de température dans vos circuits, et bien plus encore. Vous pouvez ensuite capturer votre schéma comme une mise en page initiale et concevoir tous les aspects de votre prochain PCB. Vous disposerez également d'un ensemble complet d'outils pour documenter tous les aspects de votre projet, gérer votre chaîne d'approvisionnement et préparer les livrables pour votre fabricant.

Vous pouvez maintenant télécharger un essai gratuit d'Altium Designer et en apprendre davantage sur les meilleurs outils de mise en page, de simulation et de planification de production de l'industrie. Parlez dès aujourd'hui à un expert d'Altium pour en savoir plus.