Funzione di trasferimento del filtro e analisi polo-zero in Altium Designer

Ricordo di aver trascorso ore sui problemi di analisi dei circuiti nelle mie classi di elettronica, e ho imparato ad analizzare a mano tutte le sorti di configurazioni di filtri/amplificatori. I circuiti erano solitamente trattabili con la legge di Ohm e le leggi di Kirchoff, finché non c'era feedback nel circuito. I circuiti per applicazioni avanzate, come i circuiti di adattamento wideband o multiband per componenti RF, possono rapidamente diventare difficili da analizzare a mano.

Ma quando il numero di frequenze di risonanza in un filtro complesso supera 2 o 3, il problema può rapidamente diventare intrattabile. A questo punto, il problema di solito comporta la decomposizione o la soluzione diretta di un polinomio di terzo grado o superiore, il che diventa ingestibile a mano. Anche da appassionato di matematica, non sono un fan dei problemi con polinomi di grado superiore. Fortunatamente, quando si ha a che fare con filtri complessi, si possono determinare molti aspetti del comportamento del segnale

Analizzando un Circuito di Filtro Complesso

Il circuito mostrato nello schema sottostante è un filtro piuttosto complesso. Sebbene potresti non incontrare questo tipo di filtro nella pratica generale, ti avvicinerai molto quando stai progettando un circuito di adattamento per un'antenna multibanda. In questo circuito, la sorgente (V2) invia un segnale in un filtro passa-banda, e l'uscita da questa parte (la tensione attraverso il condensatore) è inserita nel filtro elimina-banda. La tensione di uscita dal filtro è misurata attraverso L3 e C3. Questo circuito di filtro è stato costruito utilizzando i componenti generici nella libreria Miscellaneous Devices.IntLib. La sorgente sinusoidale (V2) può essere trovata nella libreria Simulation Sources.IntLib.

Un'analisi semplice di questo filtro direbbe che ci sono due poli importanti; un picco nella tensione di uscita alla frequenza di risonanza RLC del passa-banda, e uno zero nella tensione di uscita alla frequenza di risonanza del elimina-banda. In realtà, questo non è corretto. Questo perché anche il condensatore C1 e l'induttore L1 partecipano alla risonanza con la parte elimina-banda di questo circuito, creando una struttura di risonanza complicata nella funzione di trasferimento del circuito.

Come vedremo, ci sono più di due picchi e zeri nella funzione di trasferimento del filtro. Questo viene normalmente fatto convertendo il circuito e il segnale di ingresso nel dominio di Laplace. In generale, la funzione di trasferimento può essere scritta come una frazione di prodotti, come mostrato nell'equazione qui sotto.

In questa equazione, ogni z è uno zero nella funzione di trasferimento, corrispondente a qualche frequenza e tasso di decadimento dove il circuito non è permesso di passare una tensione di uscita. Ogni p è un polo, che corrisponde a un picco nella funzione di trasferimento. Nei circuiti lineari senza feedback, i poli appariranno in coppie coniugate immaginarie o come coppie coniugate complesse complete con parte reale negativa. La parte reale di un polo ti dirà il comportamento transitorio nel circuito.

Se provi a calcolare le risonanze calcolando i punti critici nella tensione di uscita, scoprirai che devi risolvere un polinomio di sesto grado per le frequenze per determinare i punti critici. Per il circuito sopra, dovrai comunque risolvere un polinomio di sesto grado per determinare i poli in questo circuito. Sebbene questo problema sia tecnicamente risolvibile, è più veloce utilizzare un simulatore SPICE per determinare il comportamento del circuito nel dominio della frequenza. Invece di fare questo esercizio a mano, risolveremo questo problema con una simulazione SPICE in Altium Designer.

Calcolare la Funzione di Trasferimento del Filtro

Per calcolare la funzione di trasferimento per questo circuito, ho posizionato due sonde (I e V) all'ingresso e all'uscita. La corrente di ingresso sperimenta solo un'attenuazione o un'amplificazione ogni volta che il circuito risuona alle sue risonanze passabanda o stopband. Un confronto della misurazione della tensione di uscita (sonda V) viene confrontato con la tensione di ingresso a una specifica frequenza per costruire una funzione di trasferimento (vedi l'equazione sopra).

Per iniziare, apri il Pannello di Simulazione, e seleziona le sorgenti e le sonde di misura da utilizzare nell'analisi.

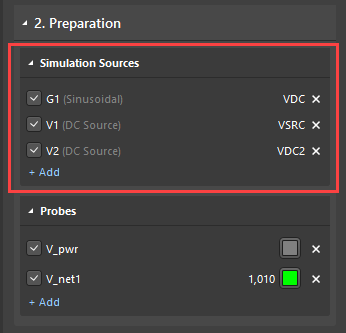
Successivamente, abilita le seguenti analisi:

• Funzione di Trasferimento: Seleziona un nome di origine e un nodo di riferimento da utilizzare per i calcoli della funzione di trasferimento nella tua rete di circuiti.
• Analisi Polo-Zero: Imposta il nodo di ingresso sulla rete con R1 (NetR1_2) e il nodo di uscita (NetC2_1). Assicurati di lasciare le opzioni del nodo di riferimento impostate su “0”, poiché ciò prenderà le misurazioni della tensione rispetto al terreno. Nota che, se ci fosse un componente da qualche parte sulla rete connesso a terra, allora dovresti cambiare queste opzioni. Le mie impostazioni sono mostrate nell'immagine qui sotto. Dai un'occhiata a questo articolo per maggiori informazioni sull'interpretazione dei risultati dell'analisi polo-zero.

Le funzioni di trasferimento dei filtri sono solitamente mostrate in un grafico di Bode. Nota che puoi estrarre direttamente la funzione di trasferimento, oppure puoi estrarre la funzione di trasferimento complessa da una scansione in AC. Un grafico di Bode è conveniente poiché mostra l'ampiezza e la fase della funzione di trasferimento nel dominio della frequenza e nello stato stazionario (dopo che tutti i transitori sono decaduti); ciò ti permette di vedere come il filtro influisce su entrambi gli aspetti importanti del comportamento del segnale di ingresso in una coppia di grafici.

Analizzando i Risultati della Tua Funzione di Trasferimento del Filtro

Una volta completata la configurazione sopra descritta, sei pronto per eseguire la tua simulazione. Premi F9 sulla tastiera o clicca su Simulate → Run Simulation. Vedrai un numero di grafici nei risultati dello sweep AC, e apparirà una finestra separata che mostra i risultati dell'analisi dei poli e degli zeri. Il circuito sopra contiene 6 poli e 2 zeri. Questi sono mostrati nell'immagine qui sotto. Nota che le unità su ciascun asse sono in unità di frequenza angolare (rad/s). Se vuoi esaminare il comportamento nei risultati dello sweep AC, allora devi convertire i valori in frequenze.

Due dei poli si trovano lungo la parte negativa dell'asse reale (cioè, non hanno parte immaginaria). Questi valori mostrano che puoi ottenere un output momentaneo dal circuito quando viene alimentato con una funzione a gradino o un impulso. Tuttavia, l'output decadrà rapidamente con due tassi di decadimento esponenziale sovrapposti. Gli altri poli e i due zeri corrispondono a specifiche frequenze, il comportamento delle quali può essere visto nei risultati dello sweep AC.

I grafici sottostanti mostrano il comportamento di questo circuito nel dominio della frequenza. Lo zero a 1,453 MHz e i poli a 800,7 kHz e 2,885 MHz sono chiaramente visibili nel grafico di Bode (curva blu nel grafico superiore). Il grafico inferiore mostra la fase della funzione di trasferimento, tuttavia, gli zeri non possono essere visti nel grafico della tensione di uscita (sovrapposto nel grafico superiore, curva viola). Il grafico della tensione di uscita mostra che i poli 3 e 4 hanno un guadagno di ~2,3, e i poli 5 e 6 hanno un guadagno di ~6.

Approfondimento con l'Analisi Transitoria

Se vuoi approfondire questa simulazione, puoi impostare la frequenza di ingresso su uno qualsiasi dei valori per i poli mostrati nel grafico di Bode ed eseguire un'analisi transitoria. Questo circuito mostra un comportamento transitorio interessante a causa del comportamento risonante complesso per le due parti di questo circuito di filtro.

È possibile osservare anche come le risposte transitorie nella corrente di ingresso e nella tensione/potenza fornita al condensatore varino nel tempo. Di seguito è mostrato un esempio. Un punto importante da ricordare qui è che questo è un circuito LTI: l'impedenza non varia nel tempo, quindi la risposta transitoria vista qui è un comportamento standard in un sistema lineare. Da questo grafico, vediamo che la tensione (e la potenza reattiva) fornita al carico capacitivo aumenterà lentamente a causa della natura reattiva complessiva di questo circuito di filtro. Potremmo certamente esaminare altre tensioni/correnti in diversi punti del circuito per vedere come si verifica questo comportamento iniziale di aumento della corrente di ingresso. Lascio questo come esercizio per il lettore.

Gli strumenti di analisi pre-layout in Altium Designer ti permettono di fare molto più che analizzare le funzioni di trasferimento dei filtri per circuiti lineari. Puoi esaminare l'immunità ai rumori, il comportamento transitorio, gli effetti della temperatura nei tuoi circuiti e molto altro. Puoi poi catturare il tuo schema come un layout iniziale e progettare tutti gli aspetti del tuo prossimo PCB. Avrai anche a disposizione un set completo di strumenti per documentare tutti gli aspetti del tuo progetto, gestire la tua catena di approvvigionamento e preparare i materiali di consegna per il tuo produttore.

Ora puoi scaricare una prova gratuita di Altium Designer e scoprire di più sui migliori strumenti di layout, simulazione e pianificazione della produzione del settore. Parla oggi con un esperto di Altium per saperne di più.