Filterübertragungsfunktion und Pol-Nullstellen-Analyse in Altium Designer

Ich erinnere mich daran, wie ich Stunden mit Schaltungsanalyseproblemen in meinen Elektronikkursen verbracht habe, und ich lernte, alle möglichen Filter-/Verstärkerkonfigurationen von Hand zu analysieren. Die Schaltungen waren in der Regel mit dem Ohmschen Gesetz und den Kirchhoffschen Gesetzen handhabbar, solange keine Rückkopplung in der Schaltung vorhanden war. Schaltungen für fortgeschrittene Anwendungen, wie breitbandige oder multibandige Anpassungsschaltungen für HF-Komponenten, können schnell schwierig werden, von Hand zu analysieren.

Aber sobald die Anzahl der Resonanzfrequenzen in einem komplexen Filter 2 oder 3 übersteigt, kann das Problem schnell unlösbar werden. An diesem Punkt beinhaltet das Problem üblicherweise die Zerlegung oder direkte Lösung eines Polynoms 3. Grades oder höher, was von Hand unhandlich wird. Selbst als Mathematiker bin ich kein Fan von Problemen mit Polynomen höheren Grades. Glücklicherweise kann man beim Umgang mit komplexen Filtern viele Aspekte des Signalverhaltens bestimmen

Die Analyse eines komplexen Filterkreises

Der im folgenden Schaltplan dargestellte Schaltkreis ist ein ziemlich komplexer Filter. Obwohl Sie diesen Typ von Filter in der allgemeinen Praxis möglicherweise nicht antreffen, werden Sie ihm ziemlich nahe kommen, wenn Sie einen Abgleichkreis für eine Multiband-Antenne entwerfen. In diesem Schaltkreis sendet die Quelle (V2) ein Signal in einen Bandpassfilter, und der Ausgang aus diesem Teil (die Spannung über dem Kondensator) wird in den Bandsperrenfilter eingespeist. Die Ausgangsspannung des Filters wird über L3 und C3 gemessen. Dieser Filterkreis wurde mit den generischen Komponenten in der Bibliothek Miscellaneous Devices.IntLib gebaut. Die sinusförmige Quelle (V2) kann in der Bibliothek Simulation Sources.IntLib gefunden werden.

Eine einfache Analyse dieses Filters würde sagen, dass es zwei wichtige Pole gibt; einen Gipfel in der Ausgangsspannung bei der Resonanzfrequenz des Bandpass-RLC und eine Nullstelle in der Ausgangsspannung bei der Resonanzfrequenz des Bandsperrenfilters. In Wirklichkeit ist dies nicht korrekt. Dies liegt daran, dass der Kondensator C1 und die Induktivität L1 auch in Resonanz mit dem Bandsperrenteil dieses Schaltkreises treten, was eine komplizierte Resonanzstruktur in der Übertragungsfunktion des Schaltkreises erzeugt.

Wie wir sehen werden, gibt es in der Übertragungsfunktion des Filters mehr als zwei Spitzen und Nullstellen. Dies wird normalerweise dadurch erreicht, dass der Schaltkreis und das Eingangssignal in den Laplace-Bereich umgewandelt werden. Allgemein kann die Übertragungsfunktion als Bruch von Produkten geschrieben werden, wie in der untenstehenden Gleichung gezeigt.

In dieser Gleichung ist jedes z eine Nullstelle in der Übertragungsfunktion, die einer bestimmten Frequenz und Abklingrate entspricht, bei der der Schaltkreis keine Ausgangsspannung durchlassen darf. Jedes p ist ein Pol, der einem Höhepunkt in der Übertragungsfunktion entspricht. In linearen Schaltkreisen ohne Rückkopplung erscheinen Pole als imaginäre konjugierte Paare oder als vollständig komplexe konjugierte Paare mit negativem Realteil. Der Realteil eines Pols gibt Ihnen das transiente Verhalten im Schaltkreis an.

Wenn Sie versuchen, die Resonanzen zu berechnen, indem Sie kritische Punkte in der Ausgangsspannung berechnen, werden Sie feststellen, dass Sie ein Polynom sechsten Grades für die Frequenzen lösen müssen, um die kritischen Punkte zu bestimmen. Für den oben genannten Schaltkreis müssen Sie immer noch ein Polynom sechsten Grades lösen, um die Pole in diesem Schaltkreis zu bestimmen. Obwohl dieses Problem technisch lösbar ist, ist es schneller, einen SPICE-Simulator zu verwenden, um das Verhalten des Schaltkreises im Frequenzbereich zu bestimmen. Anstatt diese Übung von Hand zu machen, werden wir dieses Problem mit einer SPICE-Simulation in Altium Designer lösen.

Berechnung der Filterübertragungsfunktion

Um die Übertragungsfunktion für diesen Schaltkreis zu berechnen, habe ich zwei Sonden (I und V) am Eingang und Ausgang platziert. Der Eingangsstrom wird nur eine Dämpfung oder Verstärkung erfahren, wann immer der Schaltkreis bei seinen Bandpass- oder Bandsperrenresonanzen resoniert. Ein Vergleich der Messung der Ausgangsspannung (V-Sonde) wird mit der Eingangsspannung bei einer spezifischen Frequenz verglichen, um eine Übertragungsfunktion zu konstruieren (siehe die obige Gleichung).

Um zu beginnen, öffnen Sie das Simulations-Dashboard und wählen Sie die Quellen und Messsonden aus, die in der Analyse verwendet werden sollen.

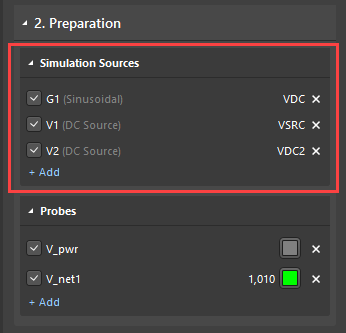
Als Nächstes aktivieren Sie die folgenden Analysen:

• Übertragungsfunktion: Wählen Sie einen Quellnamen und einen Referenzknoten für die Berechnungen der Übertragungsfunktion in Ihrem Schaltungsnetzwerk aus.
• Pole-Nullstellen-Analyse: Stellen Sie den Eingangsknoten auf das Netz mit R1 (NetR1_2) und den Ausgangsknoten (NetC2_1) ein. Achten Sie darauf, die Optionen für den Referenzknoten auf „0“ zu belassen, da dies Spannungsmessungen in Bezug auf den Boden vornimmt. Beachten Sie, dass, wenn eine Komponente irgendwo im Netz mit dem Boden verbunden wäre, Sie diese Optionen ändern müssten. Meine Einstellungen sind im Bild unten gezeigt. Schauen Sie sich diesen Artikel für weitere Informationen zur Interpretation der Ergebnisse der Pole-Nullstellen-Analyse an.

Filterübertragungsfunktionen werden üblicherweise in einem Bode-Diagramm dargestellt. Beachten Sie, dass Sie die Übertragungsfunktion direkt extrahieren können, oder Sie können die komplexe Übertragungsfunktion aus einem AC-Sweep extrahieren. Ein Bode-Diagramm ist praktisch, da es die Größe und Phase der Übertragungsfunktion im Frequenzbereich und im stationären Zustand (nachdem alle Übergänge abgeklungen sind) zeigt; dies ermöglicht es Ihnen zu sehen, wie der Filter beide wichtigen Aspekte des Verhaltens des Eingangssignals in einem Paar von Diagrammen beeinflusst.

Analyse Ihrer Filterübertragungsfunktionsergebnisse

Sobald Sie die obige Einrichtung abgeschlossen haben, sind Sie bereit, Ihre Simulation zu starten. Drücken Sie F9 auf der Tastatur oder klicken Sie auf Simulieren → Simulation starten. Sie werden eine Reihe von Diagrammen in den Ergebnissen des AC-Durchlaufs sehen, und ein separates Fenster wird erscheinen, das die Ergebnisse der Pol-Nullstellen-Analyse zeigt. Die oben dargestellte Schaltung enthält 6 Pole und 2 Nullstellen. Diese sind im Bild unten dargestellt. Beachten Sie, dass die Einheiten auf jeder Achse in Einheiten der Winkelgeschwindigkeit (rad/s) angegeben sind. Wenn Sie das Verhalten in den Ergebnissen des AC-Durchlaufs untersuchen möchten, dann müssen Sie in Frequenzwerte umrechnen.

Zwei der Pole liegen entlang des negativen Teils der reellen Achse (d.h., sie haben keinen imaginären Teil). Diese Werte zeigen, dass Sie einen momentanen Ausgang aus der Schaltung platzieren können, wenn sie mit einer Stufenfunktion oder einem Impuls gespeist wird. Allerdings wird der Ausgang schnell mit zwei überlagerten exponentiellen Abklingraten abnehmen. Die anderen Pole und die zwei Nullstellen entsprechen spezifischen Frequenzen, deren Verhalten in den Ergebnissen des AC-Durchlaufs gesehen werden kann.

Die untenstehenden Grafiken zeigen das Verhalten dieses Schaltkreises im Frequenzbereich. Die Nullstelle bei 1,453 MHz und die Pole bei 800,7 kHz und 2,885 MHz sind im Bode-Diagramm (blaue Kurve im oberen Graph) deutlich sichtbar. Der untere Graph zeigt die Phase der Übertragungsfunktion, jedoch können die Nullstellen im Ausgangsspannungsdiagramm (im oberen Graph überlagert, violette Kurve) nicht gesehen werden. Das Ausgangsspannungsdiagramm zeigt, dass die Pole 3 und 4 eine Verstärkung von ~2,3 und die Pole 5 und 6 eine Verstärkung von ~6 haben.

Mehr mit transienter Analyse

Wenn Sie mit dieser Simulation weitergehen möchten, können Sie die Eingangsfrequenz auf einen der Werte für die Pole im Bode-Diagramm setzen und eine transiente Analyse durchführen. Dieser Schaltkreis zeigt aufgrund des komplexen Resonanzverhaltens für die beiden Teile dieses Filterkreises einige interessante transiente Verhaltensweisen.

Sie können auch sehen, wie sich die transienten Antworten im Eingangsstrom und die an den Kondensator gelieferte Spannung/Leistung über die Zeit unterscheiden. Ein Beispiel wird unten gezeigt. Ein wichtiger Punkt, den man hier beachten sollte, ist, dass es sich um einen LTI-Schaltkreis handelt: Die Impedanz variiert nicht mit der Zeit, daher ist die hier gesehene transiente Antwort standardmäßiges Verhalten in einem linearen System. Aus diesem Diagramm sehen wir, dass die an die kapazitive Last gelieferte Spannung (und die Blindleistung) aufgrund der insgesamt reaktiven Natur dieses Filterschaltkreises langsam zunehmen wird. Wir könnten sicherlich auch andere Spannungen/Ströme an verschiedenen Punkten im Schaltkreis betrachten, um zu sehen, wie dieses anfängliche Ansteigen im Eingangsstrom auftritt. Ich werde dies als Übung für den Leser lassen.

Die Pre-Layout-Analysewerkzeuge in Altium Designer® ermöglichen es Ihnen, mehr zu tun, als nur Filterübertragungsfunktionen für lineare Schaltkreise zu analysieren. Sie können die Störfestigkeit, transientes Verhalten, Temperatureffekte in Ihren Schaltkreisen und vieles mehr untersuchen. Sie können dann Ihr Schaltbild als ersten Layoutentwurf erfassen und alle Aspekte Ihres nächsten PCBs entwerfen. Sie haben auch einen kompletten Satz von Werkzeugen zur Dokumentation aller Aspekte Ihres Projekts, zur Verwaltung Ihrer Lieferkette und zur Vorbereitung der Lieferdokumente für Ihren Hersteller.

Jetzt können Sie eine kostenlose Testversion von Altium Designer herunterladen und mehr über die branchenführenden Layout-, Simulations- und Produktionsplanungswerkzeuge erfahren. Sprechen Sie noch heute mit einem Altium-Experten, um mehr zu erfahren.