Decoupling Capacitor Calculations: What Size Should You Use For Digital ICs?
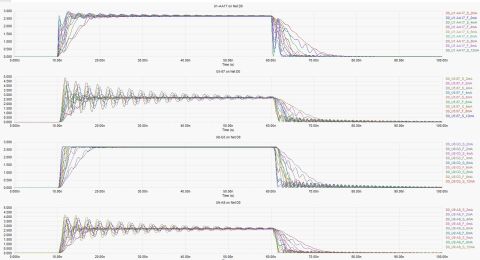
Are these decoupling capacitors sized properly?
Something that comes up repeatedly in PCB design guidelines, including high-speed digital design "gurus", is the need to find the proper decoupling capacitor size. This is sometimes addressed without a full understanding of what these caps are supposed to do in a PDN or their role in ensuring power integrity. I've also seen many application notes that default to the decades-old guideline of placing three of them to bridge power and ground pins on a digital integrated circuit (usually 1 nF, 10 nF, and 100 nF, or something like this). In the past, this was probably fine; the power integrity problems that arose in fast digital components were not so bad as to interfere with core voltages, so the job done by the three capacitors was good enough.
Today's fast integrated circuits that have multiple outputs and low core voltages (as low as 1.0 V) have much tighter noise constraints than the much slower components of yesteryear. Tighter noise constraints mean there is a need for more precise decoupling. Since this is the case, any designer working with today's reasonably powerful MCUs and many other digital components needs to know how to properly size a decoupling cap. So what is the best way to do this? In general, there are two ways to do this. Let's look at both to see how to calculate decoupling capacitor value and why the old myth of the three decoupling capacitors is not relevant in modern high-speed digital designs.
Understanding the Equivalent Capacitor Model
Before we get at into sizing the decoupling capacitors you'll need for a digital design, you’ll need to understand the basic circuit model for a capacitor. As much as we would like to think that a capacitor behaves exactly as the theory states, this is actually not the case. All capacitors have some inductance on the leads that define their impedance spectrum, which is empirically modeled as a series RLC network:
An equivalent RLC circuit used to model a capacitor
In this model, ESR and ESL are the equivalent series resistance and equivalent series inductance, respectively. The value of C can be taken as the capacitance quoted in a component’s datasheet. Finally, the value of R accounts for the conductance of the dielectric that forms the capacitor. This accounts for transient leakage that occurs in any capacitor after it is charged and removed from its circuit. This value is usually large enough that it can be ignored.
In this model (ignoring R), the value (ESR/(2*ESL)) is the damping constant of the equivalent circuit, assuming the load connected to the ends of the circuit is 0 Ohms. This is the minimum amount of time required for the circuit to respond to a change in the input voltage under full charge/discharge. Datasheets for capacitors do not list damping constants, instead, they will just show an impedance spectrum graph as shown below. If you like, you can use the ESL and ESR values in your datasheets to calculate the damping constant.
Finally, all real capacitors have a self-resonant frequency equal to the value for any series RLC circuit, or in this case:

The self-resonant frequency can be seen in an impedance spectrum graph. An example of a real AVX capacitor is shown below:

What Does a Decoupling Capacitor Actually Do?
This is a great question that really helps us understand why we need decoupling capacitors to ensure power integrity for digital integrated circuits. All capacitors store charge in equilibrium when connected to a DC voltage source; the plates in the capacitor charge up and hold a total amount of charge equal to Q = CV. If V fluctuates or drops out a little bit, then some of that charge Q is released and delivered to the load, just like a small battery.
The problem that arises in real capacitors connected to digital circuits is that the voltage dropout does not happen at a single frequency. A time-dependent fluctuation in the source voltage or a sudden burst of current into the circuit will often look like a spike with a sharp edge rate on an oscilloscope. This means the power spectrum associated with that signal will be spread across a range of frequencies and will overlap with the self-resonance. The result is that the capacitor will discharge in response and will excite a transient oscillation on the power bus. If this power is drawn into the PDN by a digital capacitor IC on the power bus, the transient on the power bus will appear as ringing at the power pin. However, if the right decoupling capacitor sizes and numbers are selected, then this fluctuation can be minimized. This is why we have the persistent guideline of the three capacitors; it's the least bad arrangement and sizing of them that can try to ensure stable power.
Methods for Sizing Decoupling Capacitors
Now that we basically know the electrical behavior of real capacitors, we can approach sizing them from three directions:
- Using load charging in the time domain: Traces on a PCB are basically capacitors, and a decoupling capacitor's job is to deliver the current a capacitor IC needs to charge up a load. You can estimate the total charge and capacitance needed to charge up traces/transmission lines using the load capacitance and the required transition time/peak voltage.
- Using the target ripple, current burst, and impedance spectrum: This requires setting limits on the power bus ringing and using this to find the capacitance needed to bring the PDN's impedance spectrum below the target impedance.
- Impulse responses in the time domain: This is where you would look at the transient response of the capacitor inside a model for the PDN. You can create phenomenological models of a PDN using your circuit schematics and use transient analysis in SPICE simulations, or you can calculate the PDN transfer function and Z-parameters using an impulse response calculation. As you iterate through various values of them, you can eventually minimize the PDN impedance below your target.
In the above list, only the first method is "simple" and can give you a baseline estimate of the total charge you would need to store in your bank of capacitors based on the minimum time required for it to deliver that charge. If you are decoupling a digital circuit that has a faster switching speed, then you will want to choose a capacitor with an equivalent damping constant that critically damps or slightly overdamps the circuit in order to suppress ringing during discharge. As long as the discharge rate is shorter than the switching time, then the decoupling cap will be able to quickly compensate for voltage fluctuations.
Estimating Total Decoupling Capacitance Based on Charging Up Traces
The simplest way to estimate the total capacitance is to consider the maximum amount of charge that needs to be delivered to a capacitor IC, how fast it should be delivered to the IC, and the size of the voltage fluctuation to be compensated. Since most loads are capacitive, you can relate the current that reaches the load to the rate at which the voltage of the signal changes from OFF to ON (or vice versa):

Note that you could apply a similar technique to a purely resistive or inductive load. Let's look at a capacitive load on a digital IC with multiple switching outputs using this formula as our decoupling capacitor calculator.
Simple Example: A Digital IC With 12 Outputs
The best way to show how to use this equation for a capacitive load is with an example. Suppose you have a digital capacitor IC with 12 outputs, where each output signal is 5 V with 6 ns rise time. Each output drives a load with 50 pF load capacitance. If you approximate the rise time of the signal as being linear, then the derivative in the above equation can be written as dV = 5 V, and dt = 6 ns. Therefore, the current required per output is:
Current per output from our example IC
If all 12 outputs were to switch from high to low simultaneously, then the total inrush of current from the PDN would be 500 mA. This inrush causes a change in the ground plane potential, which produces a change in the signal potential, and the capacitor should compensate for this change in the signal potential. If we suppose the threshold for the ON state is 4.5 V, then the voltage dip that needs to be compensated is 0.5 V in order to prevent bit errors. Furthermore, this must be compensated within 6 ns. Therefore, the minimum decoupling capacitance is:
The minimum capacitance of the example decoupling capacitor
Here, you should use—at least—a 6 nF capacitor to compensate for a 0.5 V maximum voltage within 6 ns. Note that some guidelines would recommend using two 3 nF capacitors in parallel in this example as this would reduce ESR by a factor of 2, but this will also reduce ESL by a factor of 2, so the effect on damping is nil. If the capacitor’s response is underdamped, then you may opt for a larger capacitor as this brings the response closer to the critically damped or overdamped cases. However, the use of two capacitors in parallel helps flatten the impedance spectrum of the PDN network near the capacitor’s resonance frequency.
Sizing Decoupling Capacitors from Impulse Responses/PDN Impedance
What's wrong with the above model? The problem is that it doesn't consider all the aspects of real decoupling capacitors or a real PDN in a circuit board, including:
- ESL as shown above in the equivalent capacitor impedance model
- Parasitic capacitance and inductance in the PDN
The second point is very important and requires post-layout simulations. The PDN impedance spectrum doesn't just depend on the values derived from your decoupling capacitor calculator, it also depends on the geometry of the PDN (i.e., the layer arrangement, materials, size of the buses, etc.). Because of this dependence on geometry, you'll need to export your PCB layout into a field solver utility like Ansys.
PDN Impedance With Design Exploration
This is much more difficult and is sometimes approached from a circuit model. Unfortunately, circuit models can't accurately consider real aspects of the PDN impedance, so you generally need a field solver to determine the Z-parameters, S-parameters, or other network parameters in your design. A field solver can also be used to calculate the PDN impedance spectrum, which can then be used to calculate an impulse response function with an inverse Fourier transform. This is a rather complex design exploration topic that deserves its own guide, but it is important when you start dealing with very fast components that also have low core voltages and tight noise margins.
Selecting Additional Decoupling Capacitors
Once you have this model extracted from a field solver, you can identify which portions of the PDN impedance spectrum have high impedance, and you can select additional decoupling capacitors that target those peaks in the PDN impedance spectrum. Add in capacitors that have a self-resonance that overlaps a PDN impedance peak (see below), and keep adding caps in parallel until the PDN impedance drops below the target impedance. If you're unsure of your target impedance for your PDN, read this article from Kella Knack to get a good idea of the target value you need. I'll also prepare a new article that shows how to calculate this directly.

With boards operating at lower power levels, higher data rates, and tighter noise requirements, every designer should have the tools they need for bypassing and decoupling capacitor calculation, selection, and placement for their PCBs. Only Altium Designer gives you the schematic design and layout tools you need to create new designs for any application. Altium Designer’s suite of simulation tools also helps you identify power integrity problems and examine the transient behavior of your power network.
We have only scratched the surface of what’s possible with Altium Designer on Altium 365. If you want to learn more about how to calculate decoupling capacitor values, reach out to some of our experts or start your free trial of Altium Designer + Altium 365 today.










 Back
Back