Espaciado de Pares Diferenciales y Diafonía en el Diseño de PCB

El diafonía es un aspecto fundamental de la integridad de señal, tanto en trazas de extremo único como diferencial. El espaciado entre líneas de señal con cada configuración de enrutamiento se define usando reglas generales típicas, las cuales pueden ser fácilmente definidas como reglas de diseño en tu software de diseño de PCB. Una regla general para definir el espaciado de pares diferenciales entre cada traza es la regla de “5S”, a veces llamada la regla de “5W” en notas de aplicación y otras guías de diseño de PCB.

La regla de 5S establece que el espaciado de pares diferenciales entre dos líneas debe ser un factor 5 mayor que el ancho de cada traza en el par. Cuando se requiere un enrutamiento denso para múltiples pares diferenciales, la diafonía entre pares diferenciales se convierte en una consideración importante, y necesitamos una manera de analizar el espaciado de pares diferenciales entre múltiples pares. Resulta que esto es una función de la altura de los pares al plano de tierra más cercano. Profundicemos más en esto y veamos cómo podemos determinar el espaciado correcto entre pares diferenciales para prevenir la diafonía diferencial.

¿Qué es la Diafonía Diferencial?

Como su nombre indica, el diafonía diferencial es el análogo en modo diferencial de la diafonía de extremo único, refiriéndose a formas de diafonía entre pares diferenciales, o a la diafonía generada en una traza de extremo único por un par diferencial. Los dos tipos de diafonía encontrados entre pares de extremo único (NEXT y FEXT) también ocurren entre pares diferenciales. Una fuerte diafonía diferencial puede ser inducida capacitivamente e inductivamente, dependiendo de la frecuencia y la geometría de la estructura.

El campo total visto a cierta distancia lateral del par es la suma de los campos de los dos pares. Debido a que los dos extremos de un par diferencial tienen cierto espaciado entre ellos, el campo total visto a cierta distancia lateral del par diferencial no es igual a cero. Además, la fuerza del campo electromagnético lejos de las dos trazas es mayor cuando los dos pares diferenciales tienen un espaciado mayor.

Esto motiva la formulación de alguna regla que se utiliza para definir el espaciado entre pares diferenciales entre dos pares. A partir de la discusión anterior, y simplemente sabiendo que la fuerza del campo disminuye a medida que te alejas del par, uno formularía naturalmente los siguientes requisitos de diseño para pares diferenciales:

• El espaciado entre dos pares diferenciales debe ser proporcional al espaciado entre cada traza en el par.
• La separación entre dos pares diferenciales debería ser de alguna manera proporcional a la distancia entre cada par y su plano de referencia (si es que hay alguno presente).

Veamos la siguiente geometría para dos pares diferenciales y determinemos el acoplamiento cruzado en modo diferencial entre ellos. Probablemente estés pensando que todo el punto de los pares diferenciales es la supresión de ruido; aunque esto es cierto para el ruido en modo común, la diferencia en la intensidad del campo entre las dos trazas en el par víctima producirá diferentes niveles de ruido en cada par, apareciendo como ruido en modo diferencial en el receptor.

Usando los parámetros de espaciado de par diferencial mostrados arriba, hay dos enfoques que se pueden utilizar para cuantificar el acoplamiento cruzado diferencial:

• Un modelo basado en la intensidad del campo

Calculando la Fuerza del Acoplamiento Cruzado Diferencial en un Modelo de Primer Orden

En la discusión anterior, hay otro aspecto que no se consideró: la altura de la traza sobre su plano de referencia y la disposición exacta de las trazas en el par. Consideraciones similares podrían hacerse para pares diferenciales en stripline. Aquí, nos gustaría cuantificar la fuerza del diafonía diferencial como una función de la geometría. El enfoque mostrado aquí sigue de cerca el enfoque mostrado por Doug Brooks. Esto se hace normalmente definiendo un coeficiente de diafonía a partir de un modelo de circuito. El problema con estos modelos es que no logran tener en cuenta la intensidad del campo en la traza víctima como función de la distancia entre el agresor y la víctima.

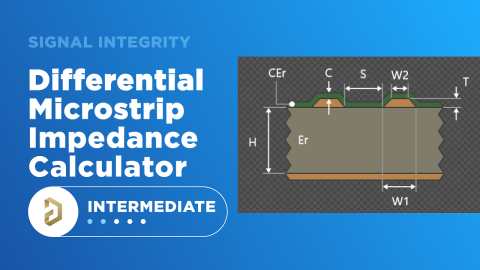
En el modelo anterior, podemos definir un coeficiente de diafonía C como función del espaciado de las trazas S y la altura sobre el plano de referencia H. Es conveniente definir el coeficiente de diafonía como una función de la relación (S/H). En este caso, el coeficiente de diafonía de extremo único entre dos trazas separadas por una distancia S con polaridad opuesta es:

Aquí, k es una constante de proporcionalidad que está relacionada con el tiempo de subida de la señal en la línea agresora, la función de transferencia de la línea víctima y la constante dieléctrica del sustrato. Alguien que haya tomado una clase de electromagnetismo sabrá que este modelo se basa en la intensidad del campo eléctrico alrededor de un cable sobre un plano conductor. Como veremos pronto, el valor de C se puede utilizar para definir la relación entre el ruido de diafonía en modo común y en modo diferencial generado en la traza víctima para una relación dada (S/H). El receptor diferencial eliminará el ruido de modo común, por lo que nos gustaría minimizar el ruido de modo diferencial.

La diafonía diferencial se define calculando sumas y diferencias en los coeficientes de diafonía. Para la disposición mostrada arriba, la diafonía entre un par diferencial y una traza en el par víctima es simplemente la suma de sus coeficientes. Note que, para cualquier valor de espaciado de par diferencial, simplemente tome la transformación de escala S → S(1+x). La diafonía diferencial es simplemente la diferencia en los coeficientes de diafonía para las trazas víctimas:

Si trazamos esto como una función de x para varios valores de (S/H), encontramos que el espaciado entre dos pares se puede reducir cuando las pistas están más cerca de un plano de tierra. La imagen a continuación muestra tal gráfico para k = 1; aumentar k simplemente mueve estas curvas hacia arriba en el eje y. Esto se hace para satisfacer un requisito dado sobre el diafonía diferencial. Por ejemplo, supongamos que requieres un coeficiente de diafonía diferencial de 0.002; si las pistas están más lejos del plano de tierra más cercano, entonces se requiere un mayor espaciado para asegurar que se cumpla este objetivo de diseño.

También, observa lo que sucede cuando (S/H) = 0.5; el coeficiente máximo de diafonía no siempre ocurre cuando x = 0. Dependiendo de tu objetivo de diseño, podrías colocar las pistas más cerca una de la otra y ver el mismo nivel de diafonía diferencial que cuando las pistas están más separadas.

Podrías estar preguntándote: ¿qué pasa con el ancho de traza? El ancho de traza es importante ya que determina la impedancia simple y diferencial, la capacitancia y la inductancia. Para una especificación de impedancia diferencial dada, un cambio en el espaciado de pares diferenciales y el grosor del sustrato obliga a un cambio en el ancho de traza para mantener el mismo valor de impedancia en modo impar.

Finalmente, deberías notar que hay un parámetro importante que falta en el modelo anterior: la constante dieléctrica. He mostrado en otras simulaciones y videos que el valor de la constante dieléctrica también importa para influir en el diafonía diferencial, y esta es una de las razones por las cuales los diseños de alta velocidad optan por valores de Dk más bajos en algunas capas. Para ver los efectos del valor de Dk en la diafonía diferencial, podrías intentar reintegrar el valor de Dk en el modelo de coeficiente de diafonía anterior, o necesitarías mirar los parámetros-S para un interconector calculados desde un solucionador de campos electromagnéticos.

Parámetros-S Multi-Puerto Para Diafonía Diferencial

Cuando utilizas un solucionador de campo para calcular el diafonía diferencial, estarás usando resultados en el dominio del tiempo (mostrando pulsos introducidos en el interconector víctima) y parámetros-S para cuantificar la diafonía diferencial de banda ancha. El primero es un enfoque de simulación estándar que se implementa en Altium Designer para trazas de extremo único, pero no para trazas diferenciales. El segundo solo es capaz de ser calculado con un solucionador de campo electromagnético.

En los resultados de la simulación a continuación, muestro un conjunto de curvas de parámetros-S extraídas con Simbeor para dos laminados comerciales (Megtron 7 y Megtron 8) en capas delgadas. El espaciado intra-par se estableció igual al ancho de las trazas en el par (S = W). El espaciado de borde a borde entre los pares varió con 1W, 2W y 3W. El grosor del dieléctrico también varió entre 1.5 mil y 3 mil.

Resultados de Megtron 7

Resultados de Megtron 8

Los resultados deberían ser muy interesantes porque ilustran que simplemente acercar la tierra a los pares diferenciales y mantener el mismo espaciado de borde de 1W etc. entre los pares diferenciales no reduce automáticamente el crosstalk. Esto se debe a que mantener 1W disminuye significativamente el espaciado de par a par. Sin embargo, pasar de un grosor de 1W/3 mil a 2W/1.5 mil todavía reduce el crosstalk y aún crea un enrutamiento de mayor densidad. Esto es exactamente lo que querríamos si estuviéramos desarrollando una placa HDI con muchas interfaces de alta velocidad provenientes del procesador principal. 

Podemos ver esto a partir de un cálculo simple con el ancho/espaciado de traza en el par y los valores de espaciado entre pares para los laminados de 3 mil y 1.5 mil.

• 3 mil Meg7 con un espaciado de 1W, S/H = 0.75, y S = 2.249 mil
  • Inicialmente Xtalk = 10.84%
• 1.5 mil Meg7 con un espaciado de 2W, S/H = 0.51, y S = 0.765 mil
  • Inicialmente Xtalk = 6.82%

Esto significa que la densidad aún aumentó un 63%, incluso con el espaciado entre pares diferenciales aumentado a 2W. Si incrementáramos el espaciado entre pares a 3W, todavía tendríamos un gran aumento en la densidad de enrutamiento.

Hay otro efecto muy importante aquí que he resaltado en los datos anteriores: la limitación de ancho de banda. La limitación de ancho de banda definida arriba se observa en la gráfica de pérdida de retorno para los interconectores; cuando la pérdida de retorno alcanza -10 dB, eso se define como el límite de ancho de banda para el canal. Podemos ver que en todos los casos anteriores, el efecto de limitación de ancho de banda en los canales se reduce al pasar a un valor de Dk más bajo. La razón por la que esto funciona es simple: te obliga a usar un ancho de traza más amplio, lo que reduce la contribución inductiva a la impedancia y disminuye la parte reactiva de la impedancia de la línea de transmisión.

Parámetros S de Modo Mixto Completo para Dos Pares Diferenciales

En algunos casos, quieres saber el nivel de ruido de modo común creado en un par diferencial debido a una señal diferencial de entrada en el par agresor. Esto se puede calcular usando parámetros S de modo mixto para nuestra red de 4 puertos mencionada anteriormente. Esto expande el número de puertos en la matriz de parámetros S a una red de 8 puertos, aunque solo 4 de estos puertos son entradas y salidas físicas. Este tipo de conjunto de parámetros S en canales diferenciales se llama parámetros S de modo mixto, y describe la conversión de modo en un solo par diferencial y entre dos pares diferenciales.

La matriz completa de parámetros S para un par diferencial que considera señales de modo común y modo diferencial es una matriz de 8x8 con la forma mostrada a continuación:

¡Esto es un montón de términos para calcular en una simulación! Los solucionadores de campo de hoy en día en herramientas de EDA pueden calcular esto examinando la señal inducida en un par diferencial víctima calculando las contribuciones de cada una de las trazas de extremo único en el par diferencial agresor. La matriz anterior describe tanto FEXT como NEXT junto con la conversión de modo (por ejemplo, FEXT visto como modo común cuando se excita por una señal diferencial de entrada). 

La moraleja de la historia es esta:

• El crosstalk diferencial crea ruido en modo diferencial y ruido en modo común en el par víctima
• En algunos casos, la minimización del ruido en modo común puede ser más importante para propósitos de EMC
  • Aumentar el espaciado del par diferencial en el par víctima es lo más efectivo para asegurar que el crosstalk sea dominante en modo diferencial
• En algunos casos, la minimización del ruido en modo diferencial puede ser más importante para propósitos de ISI
  • Disminuir el espaciado del par diferencial en el par víctima es lo más efectivo para asegurar que el crosstalk sea dominante en modo común

Puedes definir cualquier requisito de espaciado de trazas que derives como reglas de diseño cuando trabajas con Altium Designer®. Esto te ayudará a optimizar tu enrutamiento para bajo crosstalk en modo común y diferencial a lo largo de tu placa. El administrador de stackup también te permite diseñar tu apilado de capas a partir de una gama de materiales estándar, ayudando a asegurar la integridad de la señal y la integridad de la potencia.

Ahora puedes descargar una prueba gratuita de Altium Designer y aprender más sobre las mejores herramientas de diseño, simulación y planificación de producción de la industria. Habla hoy con un experto de Altium para aprender más.