Analiza biegunów i zer oraz analiza przejściowa w projektowaniu obwodów

W ramach projektowania obwodów zawsze zaleca się przeprowadzenie pewnej analizy obwodu w dziedzinie częstotliwości, czasu lub Laplace'a, aby zrozumieć zachowanie obwodu. Dziedzina czasu i Laplace'a są ze sobą powiązane w jednym obszarze: analizie przejściowej, gdzie przyglądamy się, co dzieje się z obwodem, gdy doświadcza on szybkich zmian w swoim pobudzeniu. Patrząc na funkcję przejścia w dziedzinie Laplace'a lub częstotliwości, może nie być oczywiste, jakie jest zachowanie przejściowe.

Analiza biegunów i zer polega na dekompozycji funkcji przejścia dla obwodu liniowego niezmiennego w czasie, aby określić szybkość, z jaką jego odpowiedź przejściowa zanika. Ostatecznie obwód osiąga równowagę i wykazuje swoje zachowanie w stanie ustalonym. Chociaż można to obserwować w dziedzinie czasu za pomocą symulacji przejściowej, symulacje te mogą zająć dużo czasu i muszą mieć poprawne ustawienie rozdzielczości czasu, aby osiągnąć dokładne wyniki. Analiza biegunów i zer jest szybką alternatywą, która działa w dziedzinie Laplace'a, i łatwo jest uzyskać do niej dostęp za pomocą silnika symulacji SPICE w Altium Designer.

Analiza biegunów i zer w analizie przejściowej

Analiza biegunów i zer pozwala określić stabilność jednowejściowego, jednowyjściowego systemu liniowego, poprzez obliczenie biegunów i/lub zer w funkcji przenoszenia AC dla małego sygnału obwodu. Punkt pracy DC obwodu jest znajdowany, a następnie liniowane, modele małosygnałowe dla wszystkich nieliniowych urządzeń w obwodzie są określane. Ten obwód jest następnie używany do znalezienia biegunów i zer, które spełniają funkcję przenoszenia.

Funkcja przenoszenia może pokazywać albo wzmocnienie napięciowe (napięcie wyjściowe/napięcie wejściowe), albo impedancję (napięcie wyjściowe/prąd wejściowy). Tradycyjne podejście polega na pokazywaniu wzmocnienia napięciowego. W analizie biegunów i zer faktycznie omijamy funkcję przenoszenia, aby uzyskać trzy ważne informacje:

• Stała tłumienia dla odpowiedzi przejściowej
• Częstotliwość naturalnych oscylacji dla odpowiedzi przejściowej
• Częstotliwości wymuszenia, które wykazują zerową odpowiedź

Jeśli jesteś zaznajomiony z funkcjami przejścia i transformacją Laplace'a, to już znasz ideę biegunów i zer w odpowiedzi obwodu. Analiza biegunowa opiera się na obliczaniu stałej tłumienia i częstotliwości oscylacji w obwodzie, efektywnie pokazując maksima w funkcji przejścia. Jako że większość obwodów obejmuje wyłącznie pochodne pierwszego lub drugiego rzędu ładunku w obwodzie, wynik symulacji biegunów i zer zazwyczaj ujawnia dwa możliwe bieguny w twoim obwodzie. Obwody wyższego rzędu mogą mieć znacznie więcej biegunów i/lub zer (3 lub więcej). Obliczanie tych wartości ręcznie bezpośrednio z funkcji przejścia dla bardzo skomplikowanego obwodu może być trudne, ponieważ może wymagać rozwiązania wielomianu trzeciego stopnia lub wyższego, a problem może stać się nierozwiązywalny.

Analiza biegunów i zer automatyzuje ten proces dla ciebie. Poniższy przykład pokazuje wynik analizy biegunów i zer. Jeśli spojrzymy na wykres, widzimy dwa bieguny i jedno zero. Zauważ, że części rzeczywiste tych wartości są ujemne. Dwa bieguny są zespolonymi sprzężeniami względem siebie (jak powinno być), a zero leży wzdłuż osi rzeczywistej.

Przykład i konfiguracja

Przykładowy obwód, który może być analizowany za pomocą analizy biegunów i zer, jest pokazany poniżej

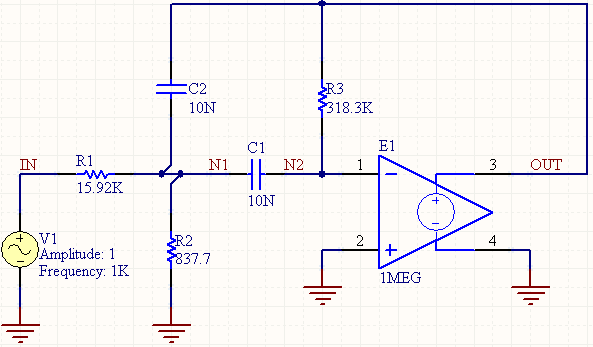
W Altium Designer, analiza biegunów i zer działa z rezystorami, kondensatorami, cewkami, źródłami sterowanymi liniowo, niezależnymi źródłami, diodami, tranzystorami BJT, MOSFETami i JFETami. Linie transmisyjne nie są obsługiwane, ale mogą być modelowane na schemacie jako obwód z elementami skupionymi, o ile znane są wartości RLCG. Przyjmuje się, że powyższy obwód ma następujące właściwości:

• Stałe wartości elementów obwodu niezależne od czasu
• E1 pracuje w zakresie liniowym (bez przesterowania)

Analiza biegunów i zer jest ustawiona w obszarze rozwijanym Analiza Ustawienia & Uruchomienie w Pulpicie symulacji (przewiń w dół do #3, kliknij wpis Analiza biegunów i zer w sekcji Zaawansowane). Przykładowa konfiguracja tego typu analizy jest pokazana na poniższym obrazie:

Obliczenie analizy biegunów i zer wymaga zdefiniowania następujących parametrów:

• Wejście węzła - dodatni węzeł wejściowy dla obwodu.
• Węzeł odniesienia wejścia - węzeł odniesienia dla wejścia obwodu (Domyślnie = 0 (GND)).
• Węzeł wyjściowy - dodatni węzeł wyjściowy dla obwodu.
• Węzeł odniesienia wyjścia - węzeł odniesienia dla wyjścia obwodu (Domyślnie = 0 (GND)).
• Typ funkcji przejścia - definiuje typ funkcji przejścia małosygnałowego AC, który ma być używany dla obwodu podczas obliczania biegunów i/lub zer. Dostępne są dwa typy:
• V(wyjście)/V(wejście) - Funkcja przejścia wzmocnienia napięciowego.
• V(wyjście)/I(wejście) - Funkcja przejścia impedancji.
• Typ analizy - pozwala dalej doprecyzować rolę analizy. Wybierz, aby znaleźć wszystkie bieguny, które spełniają funkcję przejścia dla obwodu (Tylko bieguny), wszystkie zera (Tylko zera), lub zarówno bieguny, jak i zera.

Metoda używana w analizie to suboptymalne poszukiwanie numeryczne. Dla dużych obwodów może to zająć znaczną ilość czasu lub nie udać się znaleźć wszystkich biegunów i zer. Dla niektórych obwodów metoda staje się "zagubiona" i znajduje nadmierną liczbę biegunów lub zer. Jeśli występuje brak zbieżności w znajdowaniu zarówno biegunów, jak i zer, doprecyzuj analizę do obliczania tylko biegunów lub tylko zer.

Wyniki symulacji są wyświetlane na karcie Analiza Biegunów-Zer w oknie Analizy Przebiegów.

Przykładowy wynik z analizy biegunów i zer jako część analizy przejściowej

Interpretacja wyników

Wartości na osi urojonej to naturalne częstotliwości, a oś rzeczywista oznacza szybkość zaniku przejściowego (stałą tłumienia). Położenie biegunów mówi nam cztery rzeczy w analizie przejściowej.

1. Rzeczywista część bieguna to stała tłumienia w obwodzie. Na powyższym wykresie, rzeczywista część biegunów jest ujemna, co oznacza, że odpowiedzi przejściowe będą zanikać z czasem.
2. Urojona część to częstotliwość, z jaką odpowiedź przejściowa będzie oscylować (około 1 kHz). W tym przypadku, odpowiedź przejściowa wyprodukuje oscylacje niedotłumione. Zauważ, że gdyby bieguny znajdowały się w prawej połowie wykresu (tj. rzeczywista część biegunów była dodatnia), wtedy ten system byłby niestabilny z rozbiegającym się cyklem granicznym, a odpowiedź przejściowa rosłaby z czasem.
3. Bieguny leżące na x = 0 to częstotliwości rezonansowe, które odpowiadają harmonijnemu wzbudzeniu sygnałem AC.
4. Zera funkcji przenoszenia odnoszą się do konkretnych częstotliwości, które produkują zerowe wyjście w obwodzie.

Jeśli przeprowadzisz analizę biegunów i zer i stwierdzisz, że twój obwód wykazuje niepożądaną odpowiedź (np. odpowiedź niedotłumioną w sieci dopasowania impedancji), możesz iterować przez różne wartości komponentów w swoim obwodzie, aby określić wartości komponentów, które dają pożądaną odpowiedź. Pozwala to na krytyczne tłumienie odpowiedzi w twoim obwodzie, tak aby można było wyeliminować przeregulowanie/niedoregulowanie.

Pracując z narzędziami do symulacji obwodów w Altium Designer^®, nie będziesz musiał przeprowadzać ręcznej analizy przejściowej. Narzędzia do projektowania i symulacji obwodów, układania PCB i wiele innych, będące standardem branżowym, są idealne. Te narzędzia są zintegrowane w jedną platformę, co pozwala na ich szybkie włączenie do twojego przepływu pracy.

Skontaktuj się z nami lub pobierz darmową wersję próbną, jeśli chcesz dowiedzieć się więcej o Altium Designer. Będziesz miał dostęp do najlepszych w branży narzędzi do układania, symulacji i zarządzania danymi w jednym programie. Porozmawiaj z ekspertem Altium już dziś, aby dowiedzieć się więcej.