ポール・ゼロ解析と回路設計における過渡解析

回路設計の一環として、回路の挙動を理解するために、周波数領域、時間領域、またはラプラス領域での回路解析を行うことが常に推奨されます。時間領域とラプラス領域は、過渡解析という一つの領域で関連しています。ここでは、回路がその励起に急激な変化を経験する際に何が起こるかを見ます。ラプラス領域や周波数領域で伝達関数を見ても、過渡挙動がどのようなものかは明らかではないかもしれません。

零点解析は、線形時不変回路の伝達関数を分解して、その過渡応答がどの速さで減衰するかを決定することを含みます。最終的に、回路は平衡状態に達し、その定常状態の挙動を示します。これは時間領域で過渡シミュレーションを用いて見ることができますが、これらのシミュレーションには多くの時間がかかり、正確な結果を得るためには正しい時間解像度設定が必要です。零点解析は、ラプラス領域で動作する迅速な代替手段であり、Altium DesignerのSPICEシミュレーションエンジンを通じてこれに簡単にアクセスできます。

過渡解析における零点解析

ポール・ゼロ解析を使用すると、回路の小信号AC伝達関数における極および/または零点を計算することにより、単一入力、単一出力の線形システムの安定性を判断できます。回路の直流動作点が見つかり、次に非線形デバイスのすべてに対して線形化された小信号モデルが決定されます。この回路は、伝達関数を満たす極と零点を見つけるために使用されます。

伝達関数は、電圧利得（出力電圧/入力電圧）またはインピーダンス（出力電圧/入力電流）を示すことができます。従来のアプローチは、電圧利得を示すことです。ポール・ゼロ解析では、実際に伝達関数をバイパスして、3つの重要な情報を得ます：

• 過渡応答の減衰定数
• 過渡応答の自然振動周波数
• ゼロ応答を示す励起周波数

伝達関数やラプラス変換に精通している場合、回路の応答における極と零点の概念に既に慣れているでしょう。極解析は、回路内の減衰定数と振動周波数を計算することに基づいており、伝達関数の最大値を効果的に示します。ほとんどの回路は、回路内の電荷の一次または二次導関数だけに関与しているため、極-零点シミュレーションの出力は、一般的に回路内の2つの可能な極を明らかにします。高次の回路は、多くの極や零点（3つ以上）を持つことがあります。非常に複雑な回路の伝達関数からこれらの値を手動で計算することは、三次以上の多項式を解く必要がある場合があり、問題は扱いにくくなる可能性があります。

極-零点解析は、このプロセスを自動化します。以下の例は、極-零点解析からの出力を示しています。グラフを見ると、2つの極と1つの零点があることがわかります。これらの値の実部が負であることに注意してください。2つの極は互いに複素共役（あるべき通り）であり、零点は実軸に沿っています。

例と設定

ポール・ゼロ解析で分析できる回路の例を以下に示します。

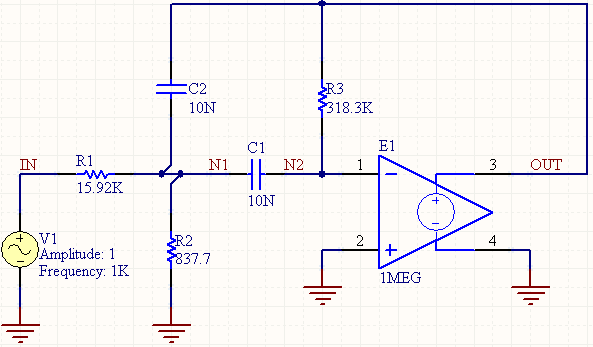
Altium Designerでは、ポール・ゼロ解析は抵抗器、コンデンサ、インダクタ、線形制御源、独立源、ダイオード、BJT、MOSFET、JFETで機能します。伝送線はサポートされていませんが、RLCG値がわかっている限り、スキーマティック内で集中要素回路としてモデル化することができます。上記の回路は、以下の特性を持つと仮定されます：

• 時不変の回路要素値
• E1は線形範囲で動作しています（レール現象なし）

ポール・ゼロ解析は、シミュレーションダッシュボードのAnalysis Setup & Runドロップダウンエリアで設定されます（#3までスクロールダウンし、AdvancedセクションのPole-Zero Analysisエントリをクリックします）。この分析タイプの例の設定は、以下の画像に示されています：

ポール・ゼロ解析計算には、以下のパラメータ定義が必要です：

• 入力ノード - 回路の正の入力ノード。
• 入力参照ノード - 回路の入力の参照ノード（デフォルト = 0 (GND)）。
• 出力ノード - 回路の正の出力ノード。
• 出力基準ノード - 回路の出力の基準ノード（デフォルト = 0 (GND)）。
• 伝達関数タイプ - 極および/または零点を計算する際に回路で使用される交流小信号伝達関数のタイプを定義します。利用可能なタイプは2つあります：
• V(出力)/V(入力) - 電圧利得伝達関数。
• V(出力)/I(入力) - インピーダンス伝達関数。
• 分析タイプ - 分析の役割をさらに洗練させることができます。回路の伝達関数を満たすすべての極（極のみ）、すべての零点（零点のみ）、または極と零点の両方を見つけることを選択します。

分析に使用される方法は、最適でない数値検索です。大きな回路では、すべての極と零点を見つけるのにかなりの時間がかかるか、または失敗することがあります。一部の回路では、この方法が「迷い」、過剰な数の極または零点を見つけます。極と零点の両方を見つける際に収束しない場合は、分析を洗練して極のみまたは零点のみを計算します。

シミュレーション結果は、波形解析ウィンドウのポール・ゼロ解析タブに表示されます。

過渡解析の一部としてのポール・ゼロ解析からの例示出力

結果の解釈

虚軸上の値は自然周波数であり、実軸は過渡減衰率（減衰定数）を示します。ポールの位置は過渡解析において4つのことを教えてくれます。

1. ポールの実部は回路の減衰定数です。上記のプロットでは、ポールの実部は負であり、過渡応答が時間とともに減衰することを意味します。
2. 虚部は過渡応答が振動する周波数（約1kHz）です。この場合、過渡応答は過小減衰振動を生じます。ポールがグラフの右半分に位置していた場合（つまり、ポールの実部が正であった場合）、このシステムは発散するリミットサイクルで不安定になり、過渡応答は時間とともに増大します。
3. x = 0に位置するポールは、AC信号で駆動するときの共振周波数に対応します。
4. 伝達関数のゼロは、回路でゼロ出力を生じる特定の周波数を指します。

ポールゼロ解析を完了し、回路が望ましくない応答（例えば、インピーダンスマッチングネットワークでの過小減衰応答）を示すことがわかった場合、異なるコンポーネント値を反復して試すことで、望ましい応答を生み出すコンポーネントの値を決定できます。これにより、回路の応答を臨界減衰させ、オーバーシュート/アンダーシュートを排除できます。

Altium Designer^®で回路シミュレーションツールを使用すると、過渡解析を手動で行う必要がありません。業界標準のレイアウトおよびシミュレーションツールは、回路設計、回路シミュレーション、PCBレイアウトなどに最適です。これらのツールは単一のプラットフォームに統合されており、ワークフローに迅速に組み込むことができます。

お問い合わせください、または無料トライアルをダウンロードして、Altium Designerについてもっと知りたい方は。業界最高のレイアウト、シミュレーション、およびデータ管理ツールにアクセスできる単一のプログラムです。今日、Altiumの専門家に相談して、さらに詳しく学びましょう。