伝送線路における位相歪みの分析方法

信号整合の主な目標は、PCB内のドライバーコンポーネントから送信された信号が、受信コンポーネントに到達する際に、二つの信号間の違いを最小限に抑えることです。受信側の信号がドライバーから送信された信号と完全に一致することはありませんが、試みることで通常は近づけることができます。極めて高速なシリアルプロトコルでは、歪みが最小限であれば、受信機は等化を通じて信号を容易に回復できます。

私たちが信号の歪みを考えるとき、アンプによって引き起こされる高調波歪みのような非線形歪みにデフォルト設定したくなることがあります。しかし、クリッピングが発生しなくても、線形チャネルも歪みを引き起こします。この線形歪みはどこから来るのでしょうか？見落とされがちな一つの形は、受信側で観測される時間領域波形を変更する伝送線の位相歪みです。では、デザイナーは伝送線上のこの歪みの形をどのように考慮すればよいのでしょうか？信号の歪みのこの側面と、それがPCB上の高速信号にとってなぜ重要であるかについて詳しく知るには、続きを読んでください。

伝送路における位相歪みとは何か？

フェーズ歪みは、PCB上の伝送線で発生することがある信号歪みの一形態です。フェーズ歪みは、PCB基板内の誘電体分散により、異なる周波数が異なる信号速度で移動する結果生じます。誘電率が周波数によって変化するため、信号速度も周波数によって変化します。その結果、実際の伝送線内の異なる周波数成分が異なる速度で移動します。

位相速度

この周波数による信号速度の変化は、位相速度を使用して定量化されます。簡単に言うと、位相速度は角周波数とインターコネクト上の伝播定数の観点から定義されます：

用語「位相速度」は、通常デジタル設計者の間で議論されることはありませんが、導波管設計者や一般的にRF設計者にとって非常に重要です。位相速度が一定（つまり、周波数の関数ではない）である場合、任意のデジタル信号のフーリエスペクトルを構成するすべての周波数成分は、同じ速度で移動します。位相速度が周波数の関数である場合、常にフェーズ歪みが発生します。実際の伝送線では、これは常に発生しますが、それが伝送線上で重大な信号整合性の問題を引き起こすかどうかは、程度とさまざまな歪みの源によります。

その他の歪みの源

上記の議論で私が言及したのは、誘電体分散による伝送路の位相歪みだけです。また、以下の歪みの原因もあります：

• 幾何学的分散：これは、伝送路の形状と伝送路の波動方程式に課された境界条件によって、実際の伝送路で発生します。
• 導波管内のモード歪み：すべての導波管には特定の固有モードがあり、伝播モードの伝播定数は、モードのカットオフ周波数のすぐ上の周波数で平方根関数になります。
• 減衰歪み：低損失の積層材でさえ、伝送路の伝播定数は複素数になります。実部と虚部の両方が周波数の関数です。
• 銅の粗さ：実際のPCB上の実際の伝送路には、常にある程度の銅の粗さがあります。銅の粗さも、スキン効果と因果関係による分散の原因となります。
• ファイバーウィーブ効果：これは、ファイバーウィーブの幾何学的形状が疑似ランダムであるため、現在も（私を含めて）研究が行われている活発な分野です。実際のPCBラミネート内のファイバーウィーブのおおよそ周期的な性質は、上記のすべての領域で分散を変更する可能性があります。
• インピーダンスマッチングと線長：信じられないかもしれませんが、インピーダンスマッチングと線長は伝送線上の歪みに影響を与えます。これは、抵抗性のインピーダンスマッチングであっても、受信コンポーネントの負荷インピーダンスが、コンポーネントの入力容量によってリアクティブであるためです。

これらの効果はすべて組み合わさって、伝送線上である総分散量を生み出し、位相歪みに寄与します。例外は減衰歪みであり、これは異なる周波数でのみ減衰を引き起こし、異なる周波数成分が同じ速度で移動しますが、移動中に異なるレベルの減衰を受けます。伝送線の挙動をうまく要約する要因が一つあります（そしてそれはSパラメーターではありません！）：伝送線の伝達関数です。

伝送線の伝達関数における位相の重要性

伝達関数の位相は、回路や伝送線において位相歪みが生じる可能性があることを示す重要な手がかりです。簡単に言うと、伝送線の伝達関数の位相が周波数の純粋な線形関数である場合、位相歪みは生じません。しかし、減衰歪みは依然として生じる可能性があります。

これをより明確に理解するために、ストリップラインを使用した実際のデータを用いた例を見てみましょう。以下のグラフは、2106 PCBラミネート上でソースと負荷のインピーダンスが50オームにマッチングされた25 cmストリップラインの伝達関数（大きさと位相）を示しています。受信機は入力容量が1 pFです（これは一部の高速コンポーネントにとってはやや高いですが、良い例です）。この伝達関数は、張ら他（2009）で導出された因果補正係数を使用しています。

大きさのグラフから、伝送線がローパスフィルターのように振る舞うことがすぐにわかります、これは期待通りです！しかし、ここでは伝達関数の位相が非線形であるため、位相歪みが生じることがわかります。

帯域制限信号を用いた例

これを明確に理解するために、1Vのデジタルパルスの入力ビットストリームに対して7次の近似を使用しました。本質的に、入力信号の帯域幅は約2GHzに制限されており、信号を回復するためには受信機に少なくとも4GHzの帯域幅が必要になります。伝達関数を使用して逆フーリエ変換を計算することにより、受信機で見られる波形と伝送線に最初に注入された波形を比較することができます：

この結果は正常ですか？伝達関数が非線形位相を持つ場合、伝送線上に顕著な位相歪みがあることがはっきりとわかります。比較のために、同じ線を見てみましょうが、伝達関数の位相をゼロに設定することにより位相速度分散をゼロに設定します。以下のグラフは、同じ手順で計算された出力信号を示しています：

すごいですね！フラットフェーズが大きな違いを生むことがはっきりとわかります！受信機での信号が期待通りに大幅に減衰しているのが見て取れますが、出力波形は入力波形の形状と非常によく一致しています。高周波成分は予想通りに減衰しますが、2 GHzの帯域制限された信号が大部分保存されており、歪みも最小限であることが明らかです。

伝送線理論に精通しているなら、ヘビサイド条件を使用して歪みを最小限に抑えた伝送線設計を決定できることをご存じでしょう。残念ながら、複数のソースからの広帯域分散の存在下では、関連する信号帯域全体でヘビサイド条件に基づいた設計を行うことは不可能で、特に現代の高速シリアルプロトコルは数十GHzにも及ぶ帯域幅を持っているためです。広帯域インターコネクト設計のこの側面については将来の記事でさらに議論を続けますが、今のところは、最小の歪みとある許容範囲内での最小のインピーダンス偏差を目指しながら、異なる伝送線設計を試すのに役立つツールを持っていることが重要です。

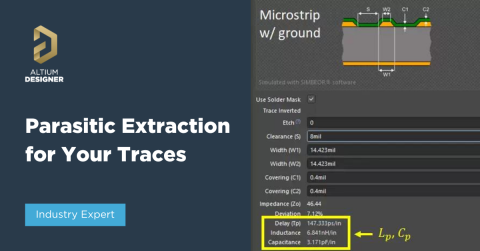
PCBデザイナーであれば、位相歪みの計算を手動で行う必要はありません。適切なPCBルーティングおよびシミュレーションツールを使用するだけです。Altium Designer®のルーティングエンジンには、Simberianからの統合電磁場ソルバーが含まれており、広帯域信号の挙動を考慮し、標準的なPCBラミネート材料や織物での最小インピーダンス偏差を持つ伝送線の設計を支援します。また、統合されたプリレイアウトおよびポストレイアウトシミュレーションツールを使用して、伝達関数を抽出し、伝送線の位相歪みを決定することもできます。

設計が完了し、プロジェクトを共有したい場合、Altium 365™プラットフォームを使用すると、他のデザイナーと簡単に協力できます。Altium DesignerとAltium 365で可能なことの表面をかすめただけです。製品ページでより詳細な機能説明を確認するか、オンデマンドウェビナーのいずれかをチェックしてください。